Forward Simulation of VRM Response on a Tree Mesh

Here we use the module SimPEG.electromagnetics.viscous_remanent_magnetization to predict the characteristic VRM response over magnetically viscous top soil. We consider a small-loop, ground-based survey which uses a coincident loop geometry. For this tutorial, we focus on the following:

• How to define the transmitters and receivers

• How to define the survey

• How to define a diagnostic physical property

• How to define the physics for the linear potential fields formulation

• How to include surface topography (if desired)

• Modeling on an OcTree mesh

Note that for this tutorial, we are only modeling the VRM response. A separate tutorial have been developed for modeling both the inductive and VRM responses.

Import modules

from SimPEG.electromagnetics import viscous_remanent_magnetization as vrm
from SimPEG.utils import plot2Ddata, surface2ind_topo
from SimPEG import maps

from discretize import TreeMesh
from discretize.utils import mkvc, refine_tree_xyz

import numpy as np
from scipy.interpolate import LinearNDInterpolator

import matplotlib.pyplot as plt
import matplotlib as mpl

# sphinx_gallery_thumbnail_number = 2

Defining Topography

Surface topography is defined as an (N, 3) numpy array. We create it here but the topography could also be loaded from a file. To keep the example simple, we set flat topography at z = 0 m.

[x_topo, y_topo, z_topo] = np.meshgrid(
    np.linspace(-100, 100, 41), np.linspace(-100, 100, 41), 0.0
)
x_topo, y_topo, z_topo = mkvc(x_topo), mkvc(y_topo), mkvc(z_topo)
xyz_topo = np.c_[x_topo, y_topo, z_topo]

Survey

Here we define the sources, the receivers and the survey. For this exercise, a coincident loop-loop system measures the vertical component of the VRM response.

# Define the transmitter waveform. This strongly determines the behaviour of the
# characteristic VRM response. Here we use a step-off. The off-time begins at
# 0 s.
waveform = vrm.waveforms.StepOff(t0=0)

# Define the time channels for the receivers. The time channels must ALL be
# ALL the off-time defined by the waveform.
time_channels = np.logspace(-4, -1, 31)

# Define the transmitter and receiver locations. This step will define the
# receivers 0.5 m above the Earth in the even you use more general topography.
x = np.linspace(-40.0, 40.0, 21)
y = np.linspace(-40.0, 40.0, 21)
x, y = np.meshgrid(x, y)
x, y = mkvc(x.T), mkvc(y.T)
fun_interp = LinearNDInterpolator(np.c_[x_topo, y_topo], z_topo)
z = fun_interp(np.c_[x, y]) + 0.5  # sensor height 0.5 m above surface.
locations = np.c_[mkvc(x), y, z]

# Define the source-receiver pairs
source_list = []
for pp in range(0, locations.shape[0]):

    # Define dbz/dt receiver
    loc_pp = np.reshape(locations[pp, :], (1, 3))
    receivers_list = [
        vrm.receivers.Point(
            loc_pp, times=time_channels, fieldType="dbdt", orientation="z"
        )
    ]

    dipole_moment = [0.0, 0.0, 1.0]

    # Define the source
    source_list.append(
        vrm.sources.MagDipole(
            receivers_list, mkvc(locations[pp, :]), dipole_moment, waveform
        )
    )

# Define the survey
survey = vrm.Survey(source_list)

Defining an OcTree Mesh

Here, we create the OcTree mesh that will be used for the tutorial. Since only the very near surface contributes significantly to the response, the dimensions of the domain in the z-direction can be small. Here, we are assuming the magnetic viscosity is negligible below 8 metres.

dx = 2  # minimum cell width (base mesh cell width) in x
dy = 2  # minimum cell width (base mesh cell width) in y
dz = 1  # minimum cell width (base mesh cell width) in z

x_length = 100.0  # domain width in x
y_length = 100.0  # domain width in y
z_length = 8.0  # domain width in y

# Compute number of base mesh cells required in x and y
nbcx = 2 ** int(np.round(np.log(x_length / dx) / np.log(2.0)))
nbcy = 2 ** int(np.round(np.log(y_length / dy) / np.log(2.0)))
nbcz = 2 ** int(np.round(np.log(z_length / dz) / np.log(2.0)))

# Define the base mesh
hx = [(dx, nbcx)]
hy = [(dy, nbcy)]
hz = [(dz, nbcz)]
mesh = TreeMesh([hx, hy, hz], x0="CCN")

# Refine based on surface topography
mesh = refine_tree_xyz(
    mesh, xyz_topo, octree_levels=[2, 2], method="surface", finalize=False
)

mesh.finalize()

Defining the Model

For the linear potential field formulation, the magnetic viscosity characterizing each cell can be defined by an “amalgamated magnetic property” (see Cowan, 2016). Here we define an amalgamated magnetic property model. The model is made by summing a set of 3D Gaussian distributions.

For other formulations of the forward simulation, you may define the parameters assuming a log-uniform or log-normal distribution of time-relaxation constants.

# Find cells active in the forward simulation (cells below surface)
ind_active = surface2ind_topo(mesh, xyz_topo)

# Define 3D Gaussian distribution parameters
xyzc = mesh.gridCC[ind_active, :]
c = 3 * np.pi * 8 ** 2
pc = np.r_[4e-4, 4e-4, 4e-4, 6e-4, 8e-4, 6e-4, 8e-4, 8e-4]
x_0 = np.r_[50.0, -50.0, -40.0, -20.0, -15.0, 20.0, -10.0, 25.0]
y_0 = np.r_[0.0, 0.0, 40.0, 10.0, -20.0, 15.0, 0.0, 0.0]
z_0 = np.r_[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
var_x = c * np.r_[3.0, 3.0, 3.0, 1.0, 3.0, 0.5, 0.1, 0.1]
var_y = c * np.r_[20.0, 20.0, 1.0, 1.0, 0.4, 0.5, 0.1, 0.4]
var_z = c * np.r_[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]

# Define model
model = np.zeros(np.shape(xyzc[:, 0]))
for ii in range(0, 8):
    model += (
        pc[ii]
        * np.exp(-((xyzc[:, 0] - x_0[ii]) ** 2) / var_x[ii])
        * np.exp(-((xyzc[:, 1] - y_0[ii]) ** 2) / var_y[ii])
        * np.exp(-((xyzc[:, 2] - z_0[ii]) ** 2) / var_z[ii])
    )

# Plot Model
mpl.rcParams.update({"font.size": 12})
fig = plt.figure(figsize=(7.5, 7))

plotting_map = maps.InjectActiveCells(mesh, ind_active, np.nan)
ax1 = fig.add_axes([0.09, 0.12, 0.72, 0.77])
mesh.plotSlice(
    plotting_map * model,
    normal="Z",
    ax=ax1,
    ind=0,
    grid=True,
    clim=(np.min(model), np.max(model)),
    pcolorOpts={"cmap": "magma_r"},
)
ax1.set_title("Model slice at z = 0 m")
ax1.set_xlabel("x (m)")
ax1.set_ylabel("y (m)")

ax2 = fig.add_axes([0.83, 0.12, 0.05, 0.77])
norm = mpl.colors.Normalize(vmin=np.min(model), vmax=np.max(model))
cbar = mpl.colorbar.ColorbarBase(
    ax2, norm=norm, orientation="vertical", cmap=mpl.cm.magma_r
)
cbar.set_label("Amalgamated Magnetic Property (SI)", rotation=270, labelpad=15, size=12)

plt.show()

Out:

/Users/josephcapriotti/codes/simpeg/tutorials/10-vrm/plot_fwd_2_vrm_topsoil.py:212: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  plt.show()

Define the Simulation

Here we define the formulation for solving Maxwell’s equations. We have chosen to model the off-time VRM response. There are two important keyword arguments, refinement_factor and refinement_distance. These are used to refine the sensitivities of the cells near the transmitters. This improves the accuracy of the forward simulation without having to refine the mesh near transmitters.

# For this example, cells lying within 2 m of a transmitter will be modeled
# as if they are comprised of 4^3 equal smaller cells. Cells within 4 m of a
# transmitter will be modeled as if they are comprised of 2^3 equal smaller
# cells.
simulation = vrm.Simulation3DLinear(
    mesh,
    survey=survey,
    indActive=ind_active,
    refinement_factor=2,
    refinement_distance=[2.0, 4.0],
)

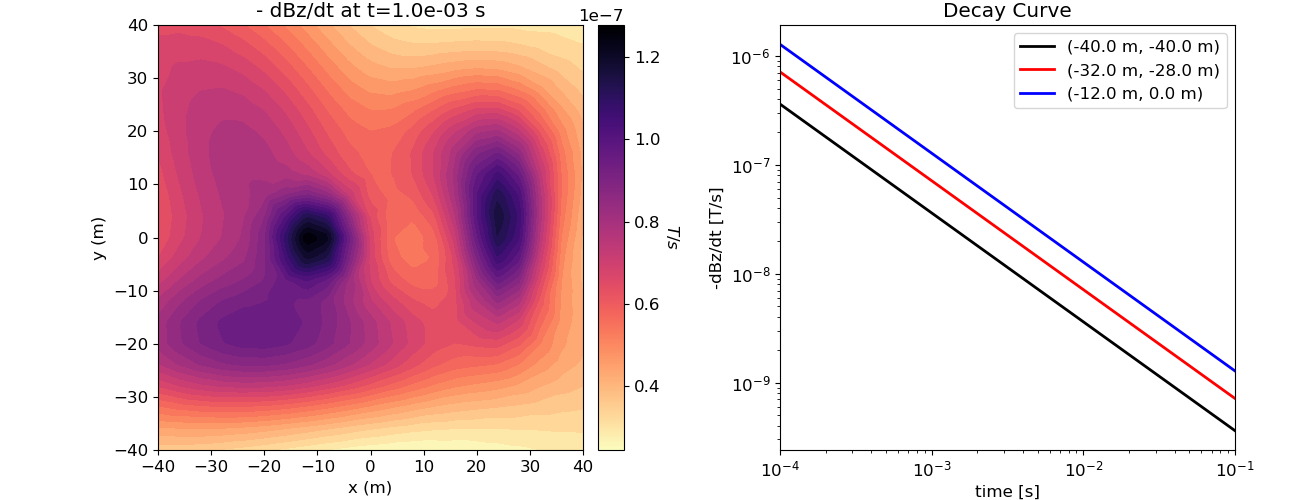
Predict Data and Plot

# Predict VRM response
dpred = simulation.dpred(model)

# Reshape for plotting
n_times = len(time_channels)
n_loc = locations.shape[0]
dpred = np.reshape(dpred, (n_loc, n_times))

# Plot
fig = plt.figure(figsize=(13, 5))

# Index for what time channel you would like to see the data map.
time_index = 10

v_max = np.max(np.abs(dpred[:, time_index]))
v_min = np.min(np.abs(dpred[:, time_index]))
ax11 = fig.add_axes([0.12, 0.1, 0.33, 0.85])
plot2Ddata(
    locations[:, 0:2],
    -dpred[:, time_index],
    ax=ax11,
    ncontour=30,
    clim=(v_min, v_max),
    contourOpts={"cmap": "magma_r"},
)
ax11.set_xlabel("x (m)")
ax11.set_ylabel("y (m)")
titlestr = "- dBz/dt at t=" + "{:.1e}".format(time_channels[time_index]) + " s"
ax11.set_title(titlestr)

ax12 = fig.add_axes([0.46, 0.1, 0.02, 0.85])
norm1 = mpl.colors.Normalize(vmin=v_min, vmax=v_max)
cbar1 = mpl.colorbar.ColorbarBase(
    ax12, norm=norm1, orientation="vertical", cmap=mpl.cm.magma_r
)
cbar1.set_label("$T/s$", rotation=270, labelpad=15, size=12)

# Indicies for some locations you would like to see the decay
location_indicies = [0, 65, 217]
color_flags = ["k", "r", "b"]
legend_str = []

ax2 = fig.add_axes([0.6, 0.1, 0.35, 0.85])
for ii in range(0, len(location_indicies)):
    ax2.loglog(time_channels, -dpred[location_indicies[ii], :], color_flags[ii], lw=2)
    legend_str.append(
        "("
        + "{:.1f}".format(locations[location_indicies[ii], 0])
        + " m, "
        + "{:.1f}".format(locations[location_indicies[ii], 1])
        + " m)"
    )

ax2.set_xlim((np.min(time_channels), np.max(time_channels)))
ax2.set_xlabel("time [s]")
ax2.set_ylabel("-dBz/dt [T/s]")
ax2.set_title("Decay Curve")
ax2.legend(legend_str)

Out:

CREATING T MATRIX
CREATING A MATRIX

<matplotlib.legend.Legend object at 0x1830a5c6d8>