Maps¶

That’s not a map…?!¶

A SimPEG map operates on a vector and transforms it to another space. We will use an example commonly applied in electromagnetics (EM) of the log-conductivity model.

\[m = \log(\sigma)\]

Here we require a mapping to get from \(m\) to \(\sigma\), we will call this map \(\mathcal{M}\).

\[\sigma = \mathcal{M}(m) = \exp(m)\]

In SimPEG, we use a (SimPEG.maps.ExpMap) to describe how to map back to conductivity. This is a relatively trivial example (we are just taking the exponential!) but by defining maps we can start to combine and manipulate exactly what we think about as our model, \(m\). In code, this looks like

M = Mesh.TensorMesh([100]) # Create a mesh
expMap = Maps.ExpMap(M)    # Create a mapping
m = np.zeros(M.nC)         # Create a model vector
m[M.vectorCCx>0.5] = 1.0   # Set half of it to 1.0
sig = expMap * m           # Apply the mapping using *
print(m)
# [ 0.    0.    0.    1.     1.     1. ]
print(sig)
# [ 1.    1.    1.  2.718  2.718  2.718]

Combining Maps¶

We will use an example where we want a 1D layered earth as our model, but we want to map this to a 2D discretization to do our forward modeling. We will also assume that we are working in log conductivity still, so after the transformation we want to map to conductivity space. To do this we will introduce the vertical 1D map (SimPEG.maps.SurjectVertical1D), which does the first part of what we just described. The second part will be done by the SimPEG.maps.ExpMap described above.

M = mesh.TensorMesh([7,5])
v1dMap = maps.SurjectVertical1D(M)
expMap = maps.ExpMap(M)
myMap = expMap * v1dMap
m = np.r_[0.2,1,0.1,2,2.9] # only 5 model parameters!
sig = myMap * m

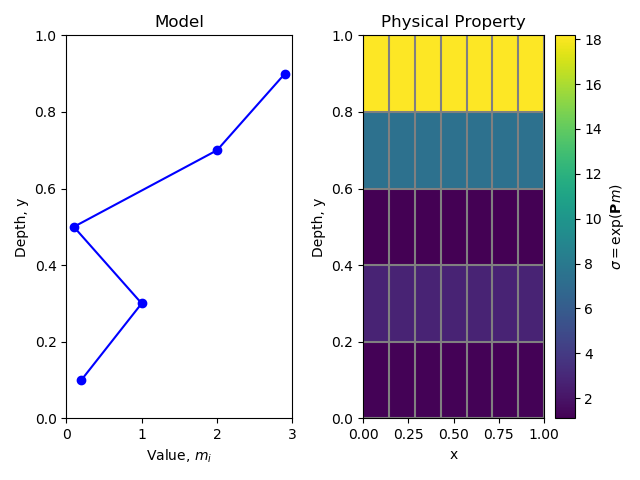
../../_images/sphx_glr_plot_combo_001.png

If you noticed, it was pretty easy to combine maps. What is even cooler is that the derivatives also are made for you (if everything goes right). Just to be sure that the derivative is correct, you should always run the test on the mapping that you create.

Taking Derivatives¶

Now that we have wrapped up the mapping, we can ensure that it is easy to take derivatives (or at least have access to them!). In the SimPEG.maps.ExpMap there are no dependencies between model parameters, so it will be a diagonal matrix:

\[\left(\frac{\partial \mathcal{M}(m)}{\partial m}\right)_{ii} = \frac{\partial \exp(m_i)}{\partial m} = \exp(m_i)\]

Or equivalently:

\[\frac{\partial \mathcal{M}(m)}{\partial m} = \text{diag}( \exp(m) )\]

The mapping API makes this really easy to test that you have got the derivative correct. When these are used in the inverse problem, this is extremely important!!

import numpy as np
import discretize
from SimPEG import maps
import matplotlib.pyplot as plt
M = discretize.TensorMesh([100])
expMap = maps.ExpMap(M)
m = np.zeros(M.nC)
m[M.vectorCCx>0.5] = 1.0
expMap.test(m, plotIt=True)

(Source code, png, hires.png, pdf)

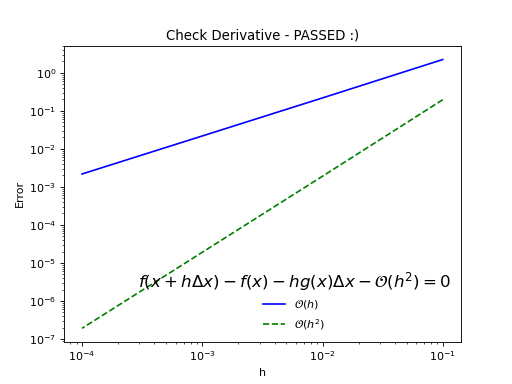
Common Maps¶

Exponential Map¶

Electrical conductivity varies over many orders of magnitude, so it is a common technique when solving the inverse problem to parameterize and optimize in terms of log conductivity. This makes sense not only because it ensures all conductivities will be positive, but because this is fundamentally the space where conductivity lives (i.e. it varies logarithmically).

class SimPEG.maps.ExpMap(*args, **kwargs)[source]

Electrical conductivity varies over many orders of magnitude, so it is a common technique when solving the inverse problem to parameterize and optimize in terms of log conductivity. This makes sense not only because it ensures all conductivities will be positive, but because this is fundamentally the space where conductivity lives (i.e. it varies logarithmically).

Changes the model into the physical property.

A common example of this is to invert for electrical conductivity in log space. In this case, your model will be log(sigma) and to get back to sigma, you can take the exponential:

\[ \begin{align}\begin{aligned}m = \log{\sigma}\\\exp{m} = \exp{\log{\sigma}} = \sigma\end{aligned}\end{align} \]

inverse(D)[source]

Parameters: D (numpy.ndarray) – physical property
Return type: numpy.ndarray
Returns: model

The transformInverse changes the physical property into the model.

\[m = \log{\sigma}\]

deriv(m, v=None)[source]

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

The transform changes the model into the physical property. The transformDeriv provides the derivative of the transform.

If the model transform is:

\[ \begin{align}\begin{aligned}m = \log{\sigma}\\\exp{m} = \exp{\log{\sigma}} = \sigma\end{aligned}\end{align} \]

Then the derivative is:

\[\frac{\partial \exp{m}}{\partial m} = \text{sdiag}(\exp{m})\]

Vertical 1D Map¶

class SimPEG.maps.SurjectVertical1D(*args, **kwargs)[source]

SurjectVertical1DMap

Given a 1D vector through the last dimension of the mesh, this will extend to the full model space.

property nP

Number of model properties.

The number of cells in the last dimension of the mesh.

deriv(m, v=None)[source]

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

Map 2D Cross-Section to 3D Model¶

class SimPEG.maps.Surject2Dto3D(*args, **kwargs)[source]

Map2Dto3D

Given a 2D vector, this will extend to the full 3D model space.

normal = 'Y': The normal

property nP

Number of model properties.

The number of cells in the last dimension of the mesh.

deriv(m, v=None)[source]

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

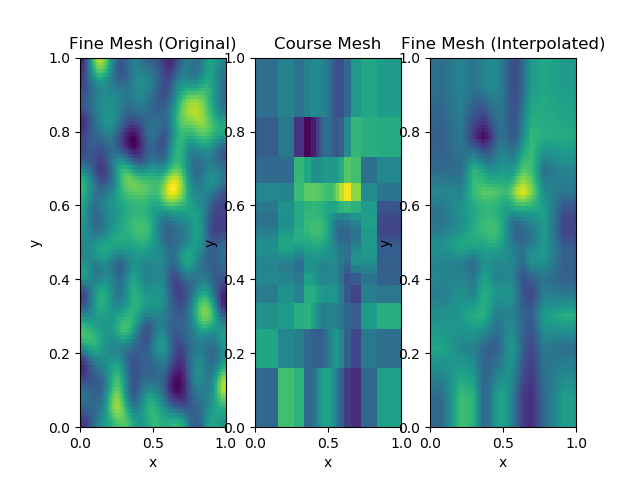
Mesh to Mesh Map¶

class SimPEG.maps.Mesh2Mesh(*args, **kwargs)[source]

Takes a model on one mesh are translates it to another mesh.

Required Properties:

indActive (Array): active indices on target mesh, a list or numpy array of <class ‘bool’> with shape (*)

property indActive: indActive (Array): active indices on target mesh, a list or numpy array of <class ‘bool’> with shape (*)

property P

property shape: Number of parameters in the model.

property nP: Number of parameters in the model.

deriv(m, v=None)[source]

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

../../_images/sphx_glr_plot_mesh2mesh_001.png

Under the Hood¶

Combo Map¶

The ComboMap holds the information for multiplying and combining maps. It also uses the chain rule to create the derivative. Remember, any time that you make your own combination of mappings be sure to test that the derivative is correct.

class SimPEG.maps.ComboMap(*args, **kwargs)[source]

Combination of various maps.

The ComboMap holds the information for multiplying and combining maps. It also uses the chain rule to create the derivative. Remember, any time that you make your own combination of mappings be sure to test that the derivative is correct.

property shape

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

property nP

Number of model properties.

The number of cells in the last dimension of the mesh.

deriv(m, v=None)[source]

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

The API¶

The IdentityMap is the base class for all mappings, and it does absolutely nothing.

class SimPEG.maps.IdentityMap(*args, **kwargs)[source]¶

Bases: properties.base.base.HasProperties

SimPEG Map

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

inverse(D)[source]¶

Changes the physical property into the model.

Note

The transformInverse may not be easy to create in general.

Parameters: D (numpy.ndarray) – physical property
Return type: numpy.ndarray
Returns: model

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

test(m=None, num=4, **kwargs)[source]¶

Test the derivative of the mapping.

Parameters

m (numpy.ndarray) – model
kwargs – key word arguments of discretize.Tests.checkDerivative()

Return type

bool

Returns

passed the test?

testVec(m=None, **kwargs)[source]¶

Test the derivative of the mapping times a vector.

Parameters

m (numpy.ndarray) – model
kwargs – key word arguments of discretize.Tests.checkDerivative()

Return type

bool

Returns

passed the test?

dot(val)[source]¶

class SimPEG.maps.ComboMap(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Combination of various maps.

The ComboMap holds the information for multiplying and combining maps. It also uses the chain rule to create the derivative. Remember, any time that you make your own combination of mappings be sure to test that the derivative is correct.

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

property nP¶

Number of model properties.

The number of cells in the last dimension of the mesh.

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.Projection(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

A map to rearrange / select parameters

Parameters

nP (int) – number of model parameters
index (numpy.ndarray) – indices to select

property shape¶: Shape of the matrix operation (number of indices x nP)

deriv(m, v=None)[source]¶

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.SumMap(*args, **kwargs)[source]¶

Bases: SimPEG.maps.ComboMap

A map to add model parameters contributing to the forward operation e.g. F(m) = F(g(x) + h(y))

Assumes that the model vectors defined by g(x) and h(y) are equal in length. Allows to assume different things about the model m: i.e. parametric + voxel models

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

property nP¶

Number of model properties.

The number of cells in the last dimension of the mesh.

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.SurjectUnits(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

A map to group model cells into homogeneous units

param list indices

list of bool for each homogeneous unit

Required Properties:

indices (a list of Array): list of indices for each unit to be surjected into, a list (each item is a list or numpy array of <class ‘bool’> with shape (*))

property indices¶: indices (a list of Array): list of indices for each unit to be surjected into, a list (each item is a list or numpy array of <class ‘bool’> with shape (*))

property P¶

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

property shape¶: Shape of the matrix operation (number of indices x nP)

deriv(m, v=None)[source]¶

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.SphericalSystem(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

A vector map to spherical parameters of amplitude, theta and phi

sphericalDeriv(model)[source]¶

inverse(model)[source]¶

Cartesian to spherical.

Parameters: model (numpy.ndarray) – physical property in Cartesian
Returns: model

property shape¶: Shape of the matrix operation (number of indices x nP)

deriv(m, v=None)[source]¶

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.Wires(*args)[source]¶

Bases: object

property nP¶

class SimPEG.maps.SelfConsistentEffectiveMedium(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap, properties.base.base.HasProperties

Two phase self-consistent effective medium theory mapping for ellipsoidal inclusions. The inversion model is the concentration (volume fraction) of the phase 2 material.

The inversion model is \(\varphi\). We solve for \(\sigma\) given \(\sigma_0\), \(\sigma_1\) and \(\varphi\) . Each of the following are implicit expressions of the effective conductivity. They are solved using a fixed point iteration.

Spherical Inclusions

If the shape of the inclusions are spheres, we use

\[\sum_{j=1}^N (\sigma^* - \sigma_j)R^{j} = 0\]

where \(j=[1,N]\) is the each material phase, and N is the number of phases. Currently, the implementation is only set up for 2 phase materials, so we solve

\[(1-\varphi)(\sigma - \sigma_0)R^{(0)} + \varphi(\sigma - \sigma_1)R^{(1)} = 0.\]

Where \(R^{(j)}\) is given by

\[R^{(j)} = \left[1 + \frac{1}{3}\frac{\sigma_j - \sigma}{\sigma} \right]^{-1}.\]

Ellipsoids

If the inclusions are aligned ellipsoids, we solve

\[\sum_{j=1}^N \varphi_j (\Sigma^* - \sigma_j\mathbf{I}) \mathbf{R}^{j, *} = 0\]

where

\[\mathbf{R}^{(j, *)} = \left[ \mathbf{I} + \mathbf{A}_j {\Sigma^{*}}^{-1}(\sigma_j \mathbf{I} - \Sigma^*) \right]^{-1}\]

and the depolarization tensor \(\mathbf{A}_j\) is given by

\[\begin{split}\mathbf{A}^* = \left[\begin{array}{ccc} Q & 0 & 0 \\ 0 & Q & 0 \\ 0 & 0 & 1-2Q \end{array}\right]\end{split}\]

for a spheroid aligned along the z-axis. For an oblate spheroid (\(\alpha < 1\), pancake-like)

\[Q = \frac{1}{2}\left( 1 + \frac{1}{\alpha^2 - 1} \left[ 1 - \frac{1}{\chi}\tan^{-1}(\chi) \right] \right)\]

where

\[\chi = \sqrt{\frac{1}{\alpha^2} - 1}\]

For reference, see Torquato (2002), Random Heterogeneous Materials

Required Properties:

alpha0 (Float): aspect ratio of the phase-0 ellipsoids, a float, Default: 1.0
alpha1 (Float): aspect ratio of the phase-1 ellipsoids, a float, Default: 1.0
maxIter (Integer): maximum number of iterations for the fixed point iteration calculation, an integer, Default: 50
orientation0 (Vector3): orientation of the phase-0 inclusions, a 3D Vector of <class ‘float’> with shape (3), Default: Z
orientation1 (Vector3): orientation of the phase-1 inclusions, a 3D Vector of <class ‘float’> with shape (3), Default: Z
random (Boolean): are the inclusions randomly oriented (True) or preferentially aligned (False)?, a boolean, Default: True
rel_tol (Float): relative tolerance for convergence for the fixed-point iteration, a float, Default: 0.001
sigma0 (Float): physical property value for phase-0 material, a float in range [0.0, inf]
sigma1 (Float): physical property value for phase-1 material, a float in range [0.0, inf]

property sigma0¶: sigma0 (Float): physical property value for phase-0 material, a float in range [0.0, inf]

property sigma1¶: sigma1 (Float): physical property value for phase-1 material, a float in range [0.0, inf]

property alpha0¶: alpha0 (Float): aspect ratio of the phase-0 ellipsoids, a float, Default: 1.0

property alpha1¶: alpha1 (Float): aspect ratio of the phase-1 ellipsoids, a float, Default: 1.0

property orientation0¶: orientation0 (Vector3): orientation of the phase-0 inclusions, a 3D Vector of <class ‘float’> with shape (3), Default: Z

property orientation1¶: orientation1 (Vector3): orientation of the phase-1 inclusions, a 3D Vector of <class ‘float’> with shape (3), Default: Z

property random¶: random (Boolean): are the inclusions randomly oriented (True) or preferentially aligned (False)?, a boolean, Default: True

property rel_tol¶: rel_tol (Float): relative tolerance for convergence for the fixed-point iteration, a float, Default: 0.001

property maxIter¶: maxIter (Integer): maximum number of iterations for the fixed point iteration calculation, an integer, Default: 50

property tol¶: absolute tolerance for the convergence of the fixed point iteration calc

property sigstart¶: first guess for sigma

wiener_bounds(phi1)[source]¶

Define Wenner Conductivity Bounds

See Torquato, 2002

hashin_shtrikman_bounds(phi1)[source]¶

Hashin Shtrikman bounds

See Torquato, 2002

hashin_shtrikman_bounds_anisotropic(phi1)[source]¶

Hashin Shtrikman bounds for anisotropic media

See Torquato, 2002

getQ(alpha)[source]¶: Geometric factor in the depolarization tensor

getA(alpha, orientation)[source]¶: Depolarization tensor

getR(sj, se, alpha, orientation=None)[source]¶: Electric field concentration tensor

getdR(sj, se, alpha, orientation=None)[source]¶: Derivative of the electric field concentration tensor with respect to the concentration of the second phase material.

deriv(m)[source]¶: Derivative of the effective conductivity with respect to the volume fraction of phase 2 material

inverse(sige)[source]¶: Compute the concentration given the effective conductivity

class SimPEG.maps.ExpMap(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Electrical conductivity varies over many orders of magnitude, so it is a common technique when solving the inverse problem to parameterize and optimize in terms of log conductivity. This makes sense not only because it ensures all conductivities will be positive, but because this is fundamentally the space where conductivity lives (i.e. it varies logarithmically).

Changes the model into the physical property.

A common example of this is to invert for electrical conductivity in log space. In this case, your model will be log(sigma) and to get back to sigma, you can take the exponential:

\[ \begin{align}\begin{aligned}m = \log{\sigma}\\\exp{m} = \exp{\log{\sigma}} = \sigma\end{aligned}\end{align} \]

inverse(D)[source]¶

Parameters: D (numpy.ndarray) – physical property
Return type: numpy.ndarray
Returns: model

The transformInverse changes the physical property into the model.

\[m = \log{\sigma}\]

deriv(m, v=None)[source]¶

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

The transform changes the model into the physical property. The transformDeriv provides the derivative of the transform.

If the model transform is:

\[ \begin{align}\begin{aligned}m = \log{\sigma}\\\exp{m} = \exp{\log{\sigma}} = \sigma\end{aligned}\end{align} \]

Then the derivative is:

\[\frac{\partial \exp{m}}{\partial m} = \text{sdiag}(\exp{m})\]

class SimPEG.maps.ReciprocalMap(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Reciprocal mapping. For example, electrical resistivity and conductivity.

\[\rho = \frac{1}{\sigma}\]

inverse(D)[source]¶

Changes the physical property into the model.

Note

The transformInverse may not be easy to create in general.

Parameters: D (numpy.ndarray) – physical property
Return type: numpy.ndarray
Returns: model

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.LogMap(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Changes the model into the physical property.

If (p) is the physical property and (m) is the model, then

\[p = \log(m)\]

and

\[m = \exp(p)\]

NOTE: If you have a model which is log conductivity (ie. (m = log(sigma))), you should be using an ExpMap

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

inverse(m)[source]¶

Changes the physical property into the model.

Note

The transformInverse may not be easy to create in general.

Parameters: D (numpy.ndarray) – physical property
Return type: numpy.ndarray
Returns: model

class SimPEG.maps.ChiMap(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Chi Map

Convert Magnetic Susceptibility to Magnetic Permeability.

\[\mu(m) = \mu_0 (1 + \chi(m))\]

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

inverse(m)[source]¶

Changes the physical property into the model.

Note

The transformInverse may not be easy to create in general.

Parameters: D (numpy.ndarray) – physical property
Return type: numpy.ndarray
Returns: model

class SimPEG.maps.MuRelative(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Invert for relative permeability

\[\mu(m) = \mu_0 * \mathbf{m}\]

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

inverse(m)[source]¶

Changes the physical property into the model.

Note

The transformInverse may not be easy to create in general.

Parameters: D (numpy.ndarray) – physical property
Return type: numpy.ndarray
Returns: model

class SimPEG.maps.Weighting(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Model weight parameters.

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

property P¶

inverse(D)[source]¶

Changes the physical property into the model.

Note

The transformInverse may not be easy to create in general.

Parameters: D (numpy.ndarray) – physical property
Return type: numpy.ndarray
Returns: model

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.ComplexMap(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

default nP is nC in the mesh times 2 [real, imag]

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.SurjectFull(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Given a scalar, the SurjectFull maps the value to the full model space.

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

deriv(m, v=None)[source]¶

Parameters: m (numpy.ndarray) – model
Return type: numpy.ndarray
Returns: derivative of transformed model

class SimPEG.maps.SurjectVertical1D(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

SurjectVertical1DMap

Given a 1D vector through the last dimension of the mesh, this will extend to the full model space.

property nP¶

Number of model properties.

The number of cells in the last dimension of the mesh.

deriv(m, v=None)[source]¶

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.Surject2Dto3D(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Map2Dto3D

Given a 2D vector, this will extend to the full 3D model space.

normal = 'Y'¶: The normal

property nP¶

Number of model properties.

The number of cells in the last dimension of the mesh.

deriv(m, v=None)[source]¶

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.Mesh2Mesh(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Takes a model on one mesh are translates it to another mesh.

Required Properties:

indActive (Array): active indices on target mesh, a list or numpy array of <class ‘bool’> with shape (*)

property indActive¶: indActive (Array): active indices on target mesh, a list or numpy array of <class ‘bool’> with shape (*)

property P¶

property shape¶: Number of parameters in the model.

property nP¶: Number of parameters in the model.

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.InjectActiveCells(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Active model parameters.

indActive = None¶: Active Cells

valInactive = None¶: Values of inactive Cells

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

property nP¶: Number of parameters in the model.

inverse(D)[source]¶

Changes the physical property into the model.

Note

The transformInverse may not be easy to create in general.

Parameters: D (numpy.ndarray) – physical property
Return type: numpy.ndarray
Returns: model

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.ParametricCircleMap(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

Parameterize the model space using a circle in a wholespace.

\[\sigma(m) = \sigma_1 + (\sigma_2 - \sigma_1)\left( \arctan\left(100*\sqrt{(\vec{x}-x_0)^2 + (\vec{y}-y_0)}-r \right) \pi^{-1} + 0.5\right)\]

Define the model as:

\[m = [\sigma_1, \sigma_2, x_0, y_0, r]\]

slope = 0.1¶

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.ParametricPolyMap(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

PolyMap

Parameterize the model space using a polynomials in a wholespace.

\[y = \mathbf{V} c\]

Define the model as:

\[m = [\sigma_1, \sigma_2, c]\]

Can take in an actInd vector to account for topography.

slope = 10000.0¶

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.ParametricSplineMap(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

SplineMap

Parameterize the boundary of two geological units using a spline interpolation

\[g = f(x)-y\]

Define the model as:

\[m = [\sigma_1, \sigma_2, y]\]

slope = 10000.0¶

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

deriv(m, v=None)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.BaseParametric(*args, **kwargs)[source]¶

Bases: SimPEG.maps.IdentityMap

slopeFact = 1¶

indActive = None¶

slope = None¶

property x¶

property y¶

property z¶

class SimPEG.maps.ParametricLayer(*args, **kwargs)[source]¶

Bases: SimPEG.maps.BaseParametric

Parametric Layer Space

m = [
    val_background,
    val_layer,
    layer_center,
    layer_thickness
]

Required

Parameters: mesh (discretize.base.BaseMesh) – SimPEG Mesh, 2D or 3D

Optional

Parameters

slopeFact (float) – arctan slope factor - divided by the minimum h spacing to give the slope of the arctan functions
slope (float) – slope of the arctan function
indActive (numpy.ndarray) – bool vector with

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

mDict(m)[source]¶

layer_cont(mDict)[source]¶

deriv(m)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.ParametricBlock(*args, **kwargs)[source]¶

Bases: SimPEG.maps.BaseParametric

Parametric Block in a Homogeneous Space

For 1D:
m = [
    val_background,
    val_block,
    block_x0,
    block_dx,
]
For 2D:
m = [
    val_background,
    val_block,
    block_x0,
    block_dx,
    block_y0,
    block_dy
]
For 3D:
m = [
    val_background,
    val_block,
    block_x0,
    block_dx,
    block_y0,
    block_dy
    block_z0,
    block_dz
]
Required

param discretize.base.BaseMesh mesh

SimPEG Mesh, 2D or 3D

Optional

param float slopeFact

arctan slope factor - divided by the minimum h spacing to give the slope of the arctan functions

param float slope

slope of the arctan function

param numpy.ndarray indActive

bool vector with active indices

Required Properties:

epsilon (Float): epsilon value used in the ekblom representation of the block, a float, Default: 1e-06
p (Float): p-value used in the ekblom representation of the block, a float, Default: 10

property epsilon¶: epsilon (Float): epsilon value used in the ekblom representation of the block, a float, Default: 1e-06

property p¶: p (Float): p-value used in the ekblom representation of the block, a float, Default: 10

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

mDict(m)[source]¶

deriv(m)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.ParametricEllipsoid(*args, **kwargs)[source]¶

Bases: SimPEG.maps.ParametricBlock

Required Properties:

epsilon (Float): epsilon value used in the ekblom representation of the block, a float, Default: 1e-06
p (Float): p-value used in the ekblom representation of the block, a float, Default: 10

class SimPEG.maps.ParametricCasingAndLayer(*args, **kwargs)[source]¶

Bases: SimPEG.maps.ParametricLayer

Parametric layered space with casing.

m = [val_background,
     val_layer,
     val_casing,
     val_insideCasing,
     layer_center,
     layer_thickness,
     casing_radius,
     casing_thickness,
     casing_bottom,
     casing_top
]

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)

mDict(m)[source]¶

casing_a(mDict)[source]¶

casing_b(mDict)[source]¶

layer_cont(mDict)[source]¶

deriv(m)[source]¶

The derivative of the transformation.

Parameters: m (numpy.ndarray) – model
Return type: scipy.sparse.csr_matrix
Returns: derivative of transformed model

class SimPEG.maps.ParametricBlockInLayer(*args, **kwargs)[source]¶

Bases: SimPEG.maps.ParametricLayer

Parametric Block in a Layered Space

For 2D:

m = [val_background,
     val_layer,
     val_block,
     layer_center,
     layer_thickness,
     block_x0,
     block_dx
]

For 3D:

m = [val_background,
     val_layer,
     val_block,
     layer_center,
     layer_thickness,
     block_x0,
     block_y0,
     block_dx,
     block_dy
]

Required

Parameters: mesh (discretize.base.BaseMesh) – SimPEG Mesh, 2D or 3D

Optional

Parameters

slopeFact (float) – arctan slope factor - divided by the minimum h spacing to give the slope of the arctan functions
slope (float) – slope of the arctan function
indActive (numpy.ndarray) – bool vector with

property nP¶

Return type: int
Returns: number of parameters that the mapping accepts

property shape¶

The default shape is (mesh.nC, nP) if the mesh is defined. If this is a meshless mapping (i.e. nP is defined independently) the shape will be the the shape (nP,nP).

Return type: tuple
Returns: shape of the operator as a tuple (int,int)