Testing SimPEG

discretize.Tests.setupMesh(meshType, nC, nDim)

For a given number of cells nc, generate a TensorMesh with uniform cells with edge length h=1/nc.

class discretize.Tests.OrderTest(methodName='runTest')

OrderTest is a base class for testing convergence orders with respect to mesh sizes of integral/differential operators.

Mathematical Problem:

Given are an operator A and its discretization A[h]. For a given test function f and h –> 0 we compare:

\[error(h) = \| A[h](f) - A(f) \|_{\infty}\]

Note that you can provide any norm.

Test is passed when estimated rate order of convergence is at least within the specified tolerance of the estimated rate supplied by the user.

Minimal example for a curl operator:

class TestCURL(OrderTest):
    name = "Curl"

    def getError(self):
        # For given Mesh, generate A[h], f and A(f) and return norm of error.


        fun  = lambda x: np.cos(x)  # i (cos(y)) + j (cos(z)) + k (cos(x))
        sol = lambda x: np.sin(x)  # i (sin(z)) + j (sin(x)) + k (sin(y))


        Ex = fun(self.M.gridEx[:, 1])
        Ey = fun(self.M.gridEy[:, 2])
        Ez = fun(self.M.gridEz[:, 0])
        f = np.concatenate((Ex, Ey, Ez))

        Fx = sol(self.M.gridFx[:, 2])
        Fy = sol(self.M.gridFy[:, 0])
        Fz = sol(self.M.gridFz[:, 1])
        Af = np.concatenate((Fx, Fy, Fz))

        # Generate DIV matrix
        Ah = self.M.edgeCurl

        curlE = Ah*E
        err = np.linalg.norm((Ah*f -Af), np.inf)
        return err

    def test_order(self):
        # runs the test
        self.orderTest()

See also: test_operatorOrder.py

name = 'Order Test'

expectedOrders = 2.0

tolerance = 0.85

meshSizes = [4, 8, 16, 32]

meshTypes = ['uniformTensorMesh']

meshDimension = 3

setupMesh(nC)

getError()

For given h, generate A[h], f and A(f) and return norm of error.

orderTest()

For number of cells specified in meshSizes setup mesh, call getError and prints mesh size, error, ratio between current and previous error, and estimated order of convergence.

discretize.Tests.Rosenbrock(x, return_g=True, return_H=True)

Rosenbrock function for testing GaussNewton scheme

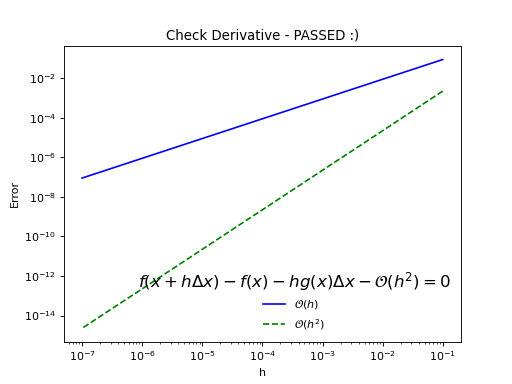
discretize.Tests.checkDerivative(fctn, x0, num=7, plotIt=True, dx=None, expectedOrder=2, tolerance=0.85, eps=1e-10, ax=None)

Basic derivative check

Compares error decay of 0th and 1st order Taylor approximation at point x0 for a randomized search direction.

Parameters

• fctn (callable) – function handle

• x0 (numpy.ndarray) – point at which to check derivative

• num (int) – number of times to reduce step length, h

• plotIt (bool) – if you would like to plot

• dx (numpy.ndarray) – step direction

• expectedOrder (int) – The order that you expect the derivative to yield.

• tolerance (float) – The tolerance on the expected order.

• eps (float) – What is zero?

Return type

bool

Returns

did you pass the test?!

from discretize import Tests, utils
import numpy as np

def simplePass(x):
    return np.sin(x), utils.sdiag(np.cos(x))
Tests.checkDerivative(simplePass, np.random.randn(5))

(Source code, png, hires.png, pdf)

discretize.Tests.getQuadratic(A, b, c=0)

Given A, b and c, this returns a quadratic, Q

\[\mathbf{Q( x ) = 0.5 x A x + b x} + c\]