\[\renewcommand{\div}{\nabla\cdot\,} \newcommand{\grad}{\vec \nabla} \newcommand{\curl}{{\vec \nabla}\times\,}\]

Frequency Domain Electromagnetics¶

Electromagnetic (EM) geophysical methods are used in a variety of applications from resource exploration, including for hydrocarbons and minerals, to environmental applications, such as groundwater monitoring. The primary physical property of interest in EM is electrical conductivity, which describes the ease with which electric current flows through a material.

Background¶

Electromagnetic phenomena are governed by Maxwell’s equations. They describe the behavior of EM fields and fluxes. Electromagnetic theory for geophysical applications by Ward and Hohmann (1988) is a highly recommended resource on this topic.

Fourier Transform Convention¶

In order to examine Maxwell’s equations in the frequency domain, we must first define our choice of harmonic time-dependence by choosing a Fourier transform convention. We use the \(e^{i \omega t}\) convention, so we define our Fourier Transform pair as

\[ \begin{align}\begin{aligned}\begin{split}F(\omega) = \int_{-\infty}^{\infty} f(t) e^{- i \omega t} dt \\\end{split}\\f(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega) e^{i \omega t} d \omega\end{aligned}\end{align} \]

where \(\omega\) is angular frequency, \(t\) is time, \(F(\omega)\) is the function defined in the frequency domain and \(f(t)\) is the function defined in the time domain.

Maxwell’s Equations¶

In the frequency domain, Maxwell’s equations are given by

\[ \begin{align}\begin{aligned}\begin{split}\curl \vec{E} + i \omega \vec{B} = \vec{S_m}\\\end{split}\\\begin{split}\curl \vec{H} - \vec{J} - i \omega \vec{D} = \vec{S_e} \\\end{split}\\\begin{split}\div \vec{B} = 0 \\\end{split}\\\div \vec{D} = \rho_f\end{aligned}\end{align} \]

where:

\(\vec{E}\) : electric field (\(V/m\) )

\(\vec{H}\) : magnetic field (\(A/m\) )

\(\vec{B}\) : magnetic flux density (\(Wb/m^2\) )

\(\vec{D}\) : electric displacement / electric flux density (\(C/m^2\) )

\(\vec{J}\) : electric current density (\(A/m^2\) )

\(\vec{S_m}\) : magnetic source term (\(V/m^2\) )

\(\vec{S_e}\) : electric source term (\(A/m^2\) )

\(\rho_f\) : free charge density (\(\Omega m\) )

Constitutive Relations¶

The fields and fluxes are related through the constitutive relations. At each frequency, they are given by

\[ \begin{align}\begin{aligned}\begin{split}\vec{J} = \sigma \vec{E} \\\end{split}\\\begin{split}\vec{B} = \mu \vec{H} \\\end{split}\\\vec{D} = \varepsilon \vec{E}\end{aligned}\end{align} \]

where:

\(\sigma\) : electrical conductivity (\(S/m\))
\(\mu\) : magnetic permeability (\(H/m\))
\(\varepsilon\) : dielectric permittivity (\(F/m\))

\(\sigma\), \(\mu\), \(\varepsilon\) are physical properties which depend on the material. \(\sigma\) describes how easily electric current passes through a material, \(\mu\) describes how easily a material is magnetized, and \(\varepsilon\) describes how easily a material is electrically polarized. In most low-frequency geophysical applications of EM, \(\sigma\) is the primary physical property of interest, and \(\mu\), \(\varepsilon\) are assumed to have their free-space values \(\mu_0 = 4\pi \times 10^{-7} H/m\) , \(\varepsilon_0 = 1/(\mu_0 c^2) \approx 8.85 \times 10^{-12} F/m\), where \(c\) is the speed of light in free space.

Quasi-static Approximation¶

For the frequency range typical of most geophysical surveys, the contribution of the electric displacement is negligible compared to the electric current density. In this case, we use the quasi-static approximation and assume that this term can be neglected, giving

\[\begin{split}\nabla \times \vec{E} + i \omega \vec{B} = \vec{S_m} \\ \nabla \times \vec{H} - \vec{J} = \vec{S_e}\end{split}\]

Geophysical methods where the quasi-static approximation, often called diffusive approximation, does not hold are high-frequency methods such as ground-penetrating radar or dielectric well-log measurements.

Implementation in SimPEG.electromagnetics¶

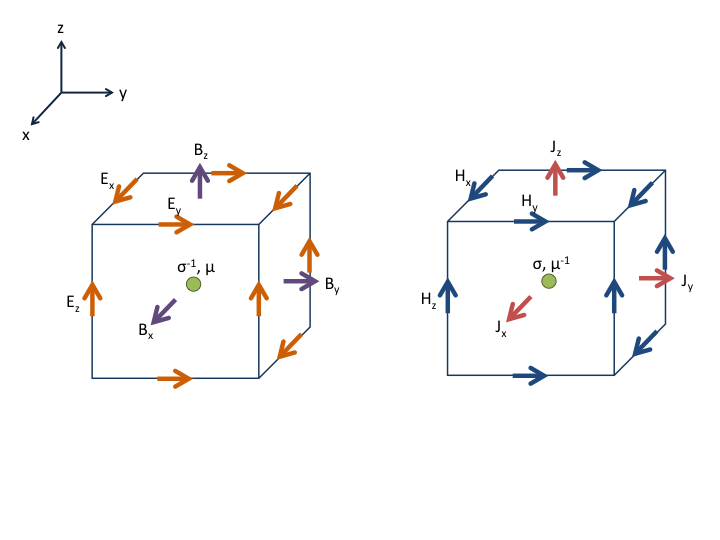
We consider two formulations in SimPEG.electromagnetics, both first-order and both in terms of one field and one flux. We allow for the definition of magnetic and electric sources (see for example: Ward and Hohmann, starting on page 144). The E-B formulation is in terms of the electric field and the magnetic flux:

\[\begin{split}\nabla \times \vec{E} + i \omega \vec{B} = \vec{S}_m \\ \nabla \times \mu^{-1} \vec{B} - \sigma \vec{E} = \vec{S}_e\end{split}\]

The H-J formulation is in terms of the current density and the magnetic field:

\[\begin{split}\nabla \times \sigma^{-1} \vec{J} + i \omega \mu \vec{H} = \vec{S}_m \\ \nabla \times \vec{H} - \vec{J} = \vec{S}_e\end{split}\]

Discretizing¶

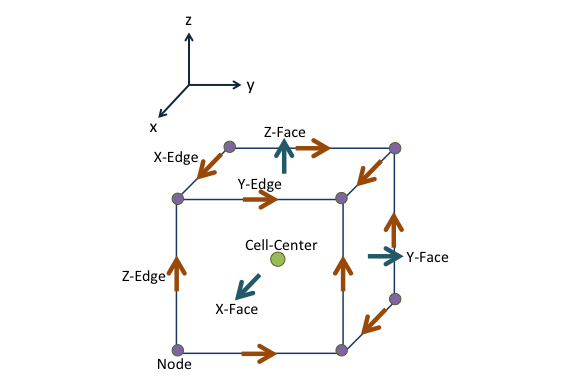
For both formulations, we use a finite volume discretization and discretize fields on cell edges, fluxes on cell faces and physical properties in cell centers. This is particularly important when using symmetry to reduce the dimensionality of a problem (for instance on a 2D CylMesh, there are \(r\), \(z\) faces and \(\theta\) edges)

For the two formulations, the discretization of the physical properties, fields and fluxes are summarized below.

Note that resistivity is the inverse of conductivity, \(\rho = \sigma^{-1}\).

E-B Formulation¶

\[\begin{split}\mathbf{C} \mathbf{e} + i \omega \mathbf{b} = \mathbf{s_m} \\ \mathbf{C^T} \mathbf{M^f_{\mu^{-1}}} \mathbf{b} - \mathbf{M^e_\sigma} \mathbf{e} = \mathbf{M^e} \mathbf{s_e}\end{split}\]

H-J Formulation¶

\[\begin{split}\mathbf{C^T} \mathbf{M^f_\rho} \mathbf{j} + i \omega \mathbf{M^e_\mu} \mathbf{h} = \mathbf{M^e} \mathbf{s_m} \\ \mathbf{C} \mathbf{h} - \mathbf{j} = \mathbf{s_e}\end{split}\]

API¶

FDEM Simulation¶

class SimPEG.electromagnetics.frequency_domain.simulation.BaseFDEMSimulation(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.base.BaseEMSimulation

We start by looking at Maxwell’s equations in the electric field \(\mathbf{e}\) and the magnetic flux density \(\mathbf{b}\)

\[\begin{split}\mathbf{C} \mathbf{e} + i \omega \mathbf{b} = \mathbf{s_m} \\ {\mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} - \mathbf{M_{\sigma}^e} \mathbf{e} = \mathbf{s_e}}\end{split}\]

if using the E-B formulation (Simulation3DElectricField or Simulation3DMagneticFluxDensity). Note that in this case, \(\mathbf{s_e}\) is an integrated quantity.

If we write Maxwell’s equations in terms of \(\mathbf{h}\) and current density \(\mathbf{j}\)

\[\begin{split}\mathbf{C}^{\top} \mathbf{M_{\rho}^f} \mathbf{j} + i \omega \mathbf{M_{\mu}^e} \mathbf{h} = \mathbf{s_m} \\ \mathbf{C} \mathbf{h} - \mathbf{j} = \mathbf{s_e}\end{split}\]

if using the H-J formulation (Simulation3DCurrentDensity or Simulation3DMagneticField). Note that here, \(\mathbf{s_m}\) is an integrated quantity.

The problem performs the elimination so that we are solving the system for \(\mathbf{e},\mathbf{b},\mathbf{j} \) or \(\mathbf{h}\)

Required Properties:

counter (Counter): A SimPEG.utils.Counter object, an instance of Counter
mesh (BaseMesh): a discretize mesh instance, an instance of BaseMesh
sensitivity_path (String): path to store the sensitivty, a unicode string, Default: ./sensitivity/
None
solver_opts (Dictionary): solver options as a kwarg dict, a dictionary
survey (Survey): a survey object, an instance of Survey

Optional Properties:

model (Model): Inversion model., a numpy array of <class ‘float’>, <class ‘int’> with shape (*, *) or (*)
mu (PhysicalProperty): Magnetic Permeability (H/m), a physical property, Default: 1.25663706212e-06
muMap (Mapping): Mapping of Magnetic Permeability (H/m) to the inversion model., a SimPEG Map
mui (PhysicalProperty): Inverse Magnetic Permeability (m/H), a physical property
muiMap (Mapping): Mapping of Inverse Magnetic Permeability (m/H) to the inversion model., a SimPEG Map
rho (PhysicalProperty): Electrical resistivity (Ohm m), a physical property
rhoMap (Mapping): Mapping of Electrical resistivity (Ohm m) to the inversion model., a SimPEG Map
sigma (PhysicalProperty): Electrical conductivity (S/m), a physical property
sigmaMap (Mapping): Mapping of Electrical conductivity (S/m) to the inversion model., a SimPEG Map

Other Properties:

muDeriv (Derivative): Derivative of Magnetic Permeability (H/m) wrt the model.
muiDeriv (Derivative): Derivative of Inverse Magnetic Permeability (m/H) wrt the model.
rhoDeriv (Derivative): Derivative of Electrical resistivity (Ohm m) wrt the model.
sigmaDeriv (Derivative): Derivative of Electrical conductivity (S/m) wrt the model.

fieldsPair[source]¶: alias of SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM

property mu¶: Magnetic Permeability (H/m)

property muMap¶: Mapping of Magnetic Permeability (H/m) to the inversion model.

property muDeriv¶: Derivative of Magnetic Permeability (H/m) wrt the model.

property mui¶: Inverse Magnetic Permeability (m/H)

property muiMap¶: Mapping of Inverse Magnetic Permeability (m/H) to the inversion model.

property muiDeriv¶: Derivative of Inverse Magnetic Permeability (m/H) wrt the model.

property survey¶: survey (Survey): a survey object, an instance of Survey

fields(m=None)[source]¶

Solve the forward problem for the fields.

Parameters: m (numpy.ndarray) – inversion model (nP,)
Return type: numpy.ndarray
Return f: forward solution

Jvec(m, v, f=None)[source]¶

Sensitivity times a vector.

Parameters

m (numpy.ndarray) – inversion model (nP,)
v (numpy.ndarray) – vector which we take sensitivity product with (nP,)
u (SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM) – fields object

Return type

numpy.ndarray

Returns

Jv (ndata,)

Jtvec(m, v, f=None)[source]¶

Sensitivity transpose times a vector

Parameters

m (numpy.ndarray) – inversion model (nP,)
v (numpy.ndarray) – vector which we take adjoint product with (nP,)
u (SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM) – fields object

Return type

numpy.ndarray

Returns

Jv (ndata,)

getSourceTerm(freq)[source]¶

Evaluates the sources for a given frequency and puts them in matrix form

Parameters: freq (float) – Frequency
Return type: tuple
Returns: (s_m, s_e) (nE or nF, nSrc)

class SimPEG.electromagnetics.frequency_domain.simulation.Simulation3DElectricField(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.simulation.BaseFDEMSimulation

By eliminating the magnetic flux density using

\[\mathbf{b} = \frac{1}{i \omega}\left(-\mathbf{C} \mathbf{e} + \mathbf{s_m}\right)\]

we can write Maxwell’s equations as a second order system in \(\mathbf{e}\) only:

\[\left(\mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{C} + i \omega \mathbf{M^e_{\sigma}} \right)\mathbf{e} = \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f}\mathbf{s_m} - i\omega\mathbf{M^e}\mathbf{s_e}\]

which we solve for \(\mathbf{e}\).

param discretize.base.BaseMesh mesh

mesh

Required Properties:

counter (Counter): A SimPEG.utils.Counter object, an instance of Counter
mesh (BaseMesh): a discretize mesh instance, an instance of BaseMesh
sensitivity_path (String): path to store the sensitivty, a unicode string, Default: ./sensitivity/
None
solver_opts (Dictionary): solver options as a kwarg dict, a dictionary
survey (Survey): a survey object, an instance of Survey

Optional Properties:

model (Model): Inversion model., a numpy array of <class ‘float’>, <class ‘int’> with shape (*, *) or (*)
mu (PhysicalProperty): Magnetic Permeability (H/m), a physical property, Default: 1.25663706212e-06
muMap (Mapping): Mapping of Magnetic Permeability (H/m) to the inversion model., a SimPEG Map
mui (PhysicalProperty): Inverse Magnetic Permeability (m/H), a physical property
muiMap (Mapping): Mapping of Inverse Magnetic Permeability (m/H) to the inversion model., a SimPEG Map
rho (PhysicalProperty): Electrical resistivity (Ohm m), a physical property
rhoMap (Mapping): Mapping of Electrical resistivity (Ohm m) to the inversion model., a SimPEG Map
sigma (PhysicalProperty): Electrical conductivity (S/m), a physical property
sigmaMap (Mapping): Mapping of Electrical conductivity (S/m) to the inversion model., a SimPEG Map

Other Properties:

muDeriv (Derivative): Derivative of Magnetic Permeability (H/m) wrt the model.
muiDeriv (Derivative): Derivative of Inverse Magnetic Permeability (m/H) wrt the model.
rhoDeriv (Derivative): Derivative of Electrical resistivity (Ohm m) wrt the model.
sigmaDeriv (Derivative): Derivative of Electrical conductivity (S/m) wrt the model.

fieldsPair[source]¶: alias of SimPEG.electromagnetics.frequency_domain.fields.Fields3DElectricField

getA(freq)[source]¶

System matrix

\[\mathbf{A} = \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{C} + i \omega \mathbf{M^e_{\sigma}}\]

Parameters: freq (float) – Frequency
Return type: scipy.sparse.csr_matrix
Returns: A

getADeriv_sigma(freq, u, v, adjoint=False)[source]¶

Product of the derivative of our system matrix with respect to the conductivity model and a vector

\[\frac{\mathbf{A}(\mathbf{m}) \mathbf{v}}{d \mathbf{m}_{\sigma}} = i \omega \frac{d \mathbf{M^e_{\sigma}}(\mathbf{u})\mathbf{v} }{d\mathbf{m}}\]

Parameters

freq (float) – frequency
u (numpy.ndarray) – solution vector (nE,)
v (numpy.ndarray) – vector to take prodct with (nP,) or (nD,) for adjoint
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

derivative of the system matrix times a vector (nP,) or adjoint (nD,)

getADeriv_mui(freq, u, v, adjoint=False)[source]¶: Product of the derivative of the system matrix with respect to the permeability model and a vector.

\[\frac{\mathbf{A}(\mathbf{m}) \mathbf{v}}{d \mathbf{m}_{\mu^{-1}} = \mathbf{C}^{ op} \frac{d \mathbf{M^f_{\mu^{-1}}}\mathbf{v}}{d\mathbf{m}}\]

getADeriv(freq, u, v, adjoint=False)[source]¶

getRHS(freq)[source]¶

Right hand side for the system

\[\mathbf{RHS} = \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f}\mathbf{s_m} - i\omega\mathbf{M_e}\mathbf{s_e}\]

Parameters: freq (float) – Frequency
Return type: numpy.ndarray
Returns: RHS (nE, nSrc)

getRHSDeriv(freq, src, v, adjoint=False)[source]¶: Derivative of the Right-hand side with respect to the model. This includes calls to derivatives in the sources

class SimPEG.electromagnetics.frequency_domain.simulation.Simulation3DMagneticFluxDensity(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.simulation.BaseFDEMSimulation

We eliminate \(\mathbf{e}\) using

\[\mathbf{e} = \mathbf{M^e_{\sigma}}^{-1} \left(\mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} - \mathbf{s_e}\right)\]

and solve for \(\mathbf{b}\) using:

\[\left(\mathbf{C} \mathbf{M^e_{\sigma}}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} + i \omega \right)\mathbf{b} = \mathbf{s_m} + \mathbf{M^e_{\sigma}}^{-1}\mathbf{M^e}\mathbf{s_e}\]

Note

The inverse problem will not work with full anisotropy

param discretize.base.BaseMesh mesh

mesh

Required Properties:

counter (Counter): A SimPEG.utils.Counter object, an instance of Counter
mesh (BaseMesh): a discretize mesh instance, an instance of BaseMesh
sensitivity_path (String): path to store the sensitivty, a unicode string, Default: ./sensitivity/
None
solver_opts (Dictionary): solver options as a kwarg dict, a dictionary
survey (Survey): a survey object, an instance of Survey

Optional Properties:

model (Model): Inversion model., a numpy array of <class ‘float’>, <class ‘int’> with shape (*, *) or (*)
mu (PhysicalProperty): Magnetic Permeability (H/m), a physical property, Default: 1.25663706212e-06
muMap (Mapping): Mapping of Magnetic Permeability (H/m) to the inversion model., a SimPEG Map
mui (PhysicalProperty): Inverse Magnetic Permeability (m/H), a physical property
muiMap (Mapping): Mapping of Inverse Magnetic Permeability (m/H) to the inversion model., a SimPEG Map
rho (PhysicalProperty): Electrical resistivity (Ohm m), a physical property
rhoMap (Mapping): Mapping of Electrical resistivity (Ohm m) to the inversion model., a SimPEG Map
sigma (PhysicalProperty): Electrical conductivity (S/m), a physical property
sigmaMap (Mapping): Mapping of Electrical conductivity (S/m) to the inversion model., a SimPEG Map

Other Properties:

muDeriv (Derivative): Derivative of Magnetic Permeability (H/m) wrt the model.
muiDeriv (Derivative): Derivative of Inverse Magnetic Permeability (m/H) wrt the model.
rhoDeriv (Derivative): Derivative of Electrical resistivity (Ohm m) wrt the model.
sigmaDeriv (Derivative): Derivative of Electrical conductivity (S/m) wrt the model.

fieldsPair[source]¶: alias of SimPEG.electromagnetics.frequency_domain.fields.Fields3DMagneticFluxDensity

getA(freq)[source]¶

System matrix

\[\mathbf{A} = \mathbf{C} \mathbf{M^e_{\sigma}}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} + i \omega\]

Parameters: freq (float) – Frequency
Return type: scipy.sparse.csr_matrix
Returns: A

getADeriv_sigma(freq, u, v, adjoint=False)[source]¶

Product of the derivative of our system matrix with respect to the model and a vector

\[\frac{\mathbf{A}(\mathbf{m}) \mathbf{v}}{d \mathbf{m}} = \mathbf{C} \frac{\mathbf{M^e_{\sigma}} \mathbf{v}}{d\mathbf{m}}\]

Parameters

freq (float) – frequency
u (numpy.ndarray) – solution vector (nF,)
v (numpy.ndarray) – vector to take prodct with (nP,) or (nD,) for adjoint
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

derivative of the system matrix times a vector (nP,) or adjoint (nD,)

getADeriv_mui(freq, u, v, adjoint=False)[source]¶

getADeriv(freq, u, v, adjoint=False)[source]¶

getRHS(freq)[source]¶

Right hand side for the system

\[\mathbf{RHS} = \mathbf{s_m} + \mathbf{M^e_{\sigma}}^{-1}\mathbf{s_e}\]

Parameters: freq (float) – Frequency
Return type: numpy.ndarray
Returns: RHS (nE, nSrc)

getRHSDeriv(freq, src, v, adjoint=False)[source]¶

Derivative of the right hand side with respect to the model

Parameters

freq (float) – frequency
src (SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM) – FDEM source
v (numpy.ndarray) – vector to take product with
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

product of rhs deriv with a vector

class SimPEG.electromagnetics.frequency_domain.simulation.Simulation3DCurrentDensity(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.simulation.BaseFDEMSimulation

We eliminate \(\mathbf{h}\) using

\[\mathbf{h} = \frac{1}{i \omega} \mathbf{M_{\mu}^e}^{-1} \left(-\mathbf{C}^{\top} \mathbf{M_{\rho}^f} \mathbf{j} + \mathbf{M^e} \mathbf{s_m} \right)\]

and solve for \(\mathbf{j}\) using

\[\left(\mathbf{C} \mathbf{M_{\mu}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\rho}^f} + i \omega\right)\mathbf{j} = \mathbf{C} \mathbf{M_{\mu}^e}^{-1} \mathbf{M^e} \mathbf{s_m} - i\omega\mathbf{s_e}\]

Note

This implementation does not yet work with full anisotropy!!

param discretize.base.BaseMesh mesh

mesh

Required Properties:

counter (Counter): A SimPEG.utils.Counter object, an instance of Counter
mesh (BaseMesh): a discretize mesh instance, an instance of BaseMesh
sensitivity_path (String): path to store the sensitivty, a unicode string, Default: ./sensitivity/
None
solver_opts (Dictionary): solver options as a kwarg dict, a dictionary
survey (Survey): a survey object, an instance of Survey

Optional Properties:

model (Model): Inversion model., a numpy array of <class ‘float’>, <class ‘int’> with shape (*, *) or (*)
mu (PhysicalProperty): Magnetic Permeability (H/m), a physical property, Default: 1.25663706212e-06
muMap (Mapping): Mapping of Magnetic Permeability (H/m) to the inversion model., a SimPEG Map
mui (PhysicalProperty): Inverse Magnetic Permeability (m/H), a physical property
muiMap (Mapping): Mapping of Inverse Magnetic Permeability (m/H) to the inversion model., a SimPEG Map
rho (PhysicalProperty): Electrical resistivity (Ohm m), a physical property
rhoMap (Mapping): Mapping of Electrical resistivity (Ohm m) to the inversion model., a SimPEG Map
sigma (PhysicalProperty): Electrical conductivity (S/m), a physical property
sigmaMap (Mapping): Mapping of Electrical conductivity (S/m) to the inversion model., a SimPEG Map

Other Properties:

muDeriv (Derivative): Derivative of Magnetic Permeability (H/m) wrt the model.
muiDeriv (Derivative): Derivative of Inverse Magnetic Permeability (m/H) wrt the model.
rhoDeriv (Derivative): Derivative of Electrical resistivity (Ohm m) wrt the model.
sigmaDeriv (Derivative): Derivative of Electrical conductivity (S/m) wrt the model.

fieldsPair[source]¶: alias of SimPEG.electromagnetics.frequency_domain.fields.Fields3DCurrentDensity

getA(freq)[source]¶

System matrix

\[\mathbf{A} = \mathbf{C} \mathbf{M^e_{\mu^{-1}}} \mathbf{C}^{\top} \mathbf{M^f_{\sigma^{-1}}} + i\omega\]

Parameters: freq (float) – Frequency
Return type: scipy.sparse.csr_matrix
Returns: A

getADeriv_rho(freq, u, v, adjoint=False)[source]¶

Product of the derivative of our system matrix with respect to the model and a vector

In this case, we assume that electrical conductivity, \(\sigma\) is the physical property of interest (i.e. \(\sigma\) = model.transform). Then we want

\[\frac{\mathbf{A(\sigma)} \mathbf{v}}{d \mathbf{m}} = \mathbf{C} \mathbf{M^e_{mu^{-1}}} \mathbf{C^{\top}} \frac{d \mathbf{M^f_{\sigma^{-1}}}\mathbf{v} }{d \mathbf{m}}\]

Parameters

freq (float) – frequency
u (numpy.ndarray) – solution vector (nF,)
v (numpy.ndarray) – vector to take prodct with (nP,) or (nD,) for adjoint
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

derivative of the system matrix times a vector (nP,) or adjoint (nD,)

getADeriv_mu(freq, u, v, adjoint=False)[source]¶

getADeriv(freq, u, v, adjoint=False)[source]¶

getRHS(freq)[source]¶

Right hand side for the system

\[\mathbf{RHS} = \mathbf{C} \mathbf{M_{\mu}^e}^{-1}\mathbf{s_m} - i\omega \mathbf{s_e}\]

Parameters: freq (float) – Frequency
Return type: numpy.ndarray
Returns: RHS (nE, nSrc)

getRHSDeriv(freq, src, v, adjoint=False)[source]¶

Derivative of the right hand side with respect to the model

Parameters

freq (float) – frequency
src (SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM) – FDEM source
v (numpy.ndarray) – vector to take product with
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

product of rhs deriv with a vector

class SimPEG.electromagnetics.frequency_domain.simulation.Simulation3DMagneticField(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.simulation.BaseFDEMSimulation

We eliminate \(\mathbf{j}\) using

\[\mathbf{j} = \mathbf{C} \mathbf{h} - \mathbf{s_e}\]

and solve for \(\mathbf{h}\) using

\[\left(\mathbf{C}^{\top} \mathbf{M_{\rho}^f} \mathbf{C} + i \omega \mathbf{M_{\mu}^e}\right) \mathbf{h} = \mathbf{M^e} \mathbf{s_m} + \mathbf{C}^{\top} \mathbf{M_{\rho}^f} \mathbf{s_e}\]

param discretize.base.BaseMesh mesh

mesh

Required Properties:

counter (Counter): A SimPEG.utils.Counter object, an instance of Counter
mesh (BaseMesh): a discretize mesh instance, an instance of BaseMesh
sensitivity_path (String): path to store the sensitivty, a unicode string, Default: ./sensitivity/
None
solver_opts (Dictionary): solver options as a kwarg dict, a dictionary
survey (Survey): a survey object, an instance of Survey

Optional Properties:

model (Model): Inversion model., a numpy array of <class ‘float’>, <class ‘int’> with shape (*, *) or (*)
mu (PhysicalProperty): Magnetic Permeability (H/m), a physical property, Default: 1.25663706212e-06
muMap (Mapping): Mapping of Magnetic Permeability (H/m) to the inversion model., a SimPEG Map
mui (PhysicalProperty): Inverse Magnetic Permeability (m/H), a physical property
muiMap (Mapping): Mapping of Inverse Magnetic Permeability (m/H) to the inversion model., a SimPEG Map
rho (PhysicalProperty): Electrical resistivity (Ohm m), a physical property
rhoMap (Mapping): Mapping of Electrical resistivity (Ohm m) to the inversion model., a SimPEG Map
sigma (PhysicalProperty): Electrical conductivity (S/m), a physical property
sigmaMap (Mapping): Mapping of Electrical conductivity (S/m) to the inversion model., a SimPEG Map

Other Properties:

muDeriv (Derivative): Derivative of Magnetic Permeability (H/m) wrt the model.
muiDeriv (Derivative): Derivative of Inverse Magnetic Permeability (m/H) wrt the model.
rhoDeriv (Derivative): Derivative of Electrical resistivity (Ohm m) wrt the model.
sigmaDeriv (Derivative): Derivative of Electrical conductivity (S/m) wrt the model.

fieldsPair[source]¶: alias of SimPEG.electromagnetics.frequency_domain.fields.Fields3DMagneticField

getA(freq)[source]¶

System matrix

\[\mathbf{A} = \mathbf{C}^{\top} \mathbf{M_{\rho}^f} \mathbf{C} + i \omega \mathbf{M_{\mu}^e}\]

Parameters: freq (float) – Frequency
Return type: scipy.sparse.csr_matrix
Returns: A

getADeriv_rho(freq, u, v, adjoint=False)[source]¶

Product of the derivative of our system matrix with respect to the model and a vector

\[\frac{\mathbf{A}(\mathbf{m}) \mathbf{v}}{d \mathbf{m}} = \mathbf{C}^{\top}\frac{d \mathbf{M^f_{\rho}}\mathbf{v}} {d\mathbf{m}}\]

Parameters

freq (float) – frequency
u (numpy.ndarray) – solution vector (nE,)
v (numpy.ndarray) – vector to take prodct with (nP,) or (nD,) for adjoint
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

derivative of the system matrix times a vector (nP,) or adjoint (nD,)

getADeriv_mu(freq, u, v, adjoint=False)[source]¶

getADeriv(freq, u, v, adjoint=False)[source]¶

getRHS(freq)[source]¶

Right hand side for the system

\[\mathbf{RHS} = \mathbf{M^e} \mathbf{s_m} + \mathbf{C}^{\top} \mathbf{M_{\rho}^f} \mathbf{s_e}\]

Parameters: freq (float) – Frequency
Return type: numpy.ndarray
Returns: RHS (nE, nSrc)

getRHSDeriv(freq, src, v, adjoint=False)[source]¶

Derivative of the right hand side with respect to the model

Parameters

freq (float) – frequency
src (SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM) – FDEM source
v (numpy.ndarray) – vector to take product with
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

product of rhs deriv with a vector

class SimPEG.electromagnetics.frequency_domain.simulation.Problem3D_e(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.simulation.Simulation3DElectricField

This class has been deprecated, see Simulation3DElectricField for documentation

class SimPEG.electromagnetics.frequency_domain.simulation.Problem3D_b(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.simulation.Simulation3DMagneticFluxDensity

This class has been deprecated, see Simulation3DMagneticFluxDensity for documentation

class SimPEG.electromagnetics.frequency_domain.simulation.Problem3D_h(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.simulation.Simulation3DMagneticField

This class has been deprecated, see Simulation3DMagneticField for documentation

class SimPEG.electromagnetics.frequency_domain.simulation.Problem3D_j(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.simulation.Simulation3DCurrentDensity

This class has been deprecated, see Simulation3DCurrentDensity for documentation

FDEM Survey¶

class SimPEG.electromagnetics.frequency_domain.survey.Survey(*args, **kwargs)[source]¶

Bases: SimPEG.survey.BaseSurvey

Frequency domain electromagnetic survey

Required Properties:

counter (Counter): A SimPEG counter object, an instance of Counter
source_list (a list of BaseFDEMSrc): A list of sources for the survey, a list (each item is an instance of BaseFDEMSrc)

property source_list¶: source_list (a list of BaseFDEMSrc): A list of sources for the survey, a list (each item is an instance of BaseFDEMSrc)

property frequencies¶: Frequencies in the survey

property freqs¶: frequencies.freq has been deprecated. See frequencies for documentation

property num_frequencies¶: Number of frequencies

property nFreq¶: num_frequencies.nFreq has been deprecated. See num_frequencies for documentation

property num_sources_by_frequency¶: Number of sources at each frequency

property nSrcByFreq¶: num_sources_by_frequency.nSrcByFreq has been deprecated. See num_sources_by_frequency for documentation

get_sources_by_frequency(frequency)[source]¶: Returns the sources associated with a specific frequency. :param float frequency: frequency for which we look up sources :rtype: dictionary :return: sources at the sepcified frequency

getSrcByFreq(**kwargs)[source]¶: Survey.getSrcByFreq has been deprecated. See Survey.get_sources_by_frequency for documentation

class SimPEG.electromagnetics.frequency_domain.sources.BaseFDEMSrc(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.base.BaseEMSrc

Base source class for FDEM Survey

Required Properties:

frequency (Float): frequency of the source, a float in range [0, inf]
integrate (Boolean): integrate the source term?, a boolean, Default: False
receiver_list (a list of BaseRx): receiver list, a list (each item is an instance of BaseRx)

Optional Properties:

location (SourceLocationArray): Location of the source [x, y, z] in 3D, a 1D array denoting the source location of <class ‘float’>, <class ‘int’> with shape (*)

property frequency¶: frequency (Float): frequency of the source, a float in range [0, inf]

bPrimary(simulation)[source]¶

Primary magnetic flux density

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary magnetic flux density

bPrimaryDeriv(simulation, v, adjoint=False)[source]¶

Derivative of the primary magnetic flux density

Parameters

simulation (BaseFDEMSimulation) – FDEM simulation
v (numpy.ndarray) – vector
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

primary magnetic flux density

hPrimary(simulation)[source]¶

Primary magnetic field

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary magnetic field

hPrimaryDeriv(simulation, v, adjoint=False)[source]¶

Derivative of the primary magnetic field

Parameters

simulation (BaseFDEMSimulation) – FDEM simulation
v (numpy.ndarray) – vector
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

primary magnetic flux density

ePrimary(simulation)[source]¶

Primary electric field

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary electric field

ePrimaryDeriv(simulation, v, adjoint=False)[source]¶

Derivative of the primary electric field

Parameters

simulation (BaseFDEMSimulation) – FDEM simulation
v (numpy.ndarray) – vector
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

primary magnetic flux density

jPrimary(simulation)[source]¶

Primary current density

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary current density

jPrimaryDeriv(simulation, v, adjoint=False)[source]¶

Derivative of the primary current density

Parameters

simulation (BaseFDEMSimulation) – FDEM simulation
v (numpy.ndarray) – vector
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

primary magnetic flux density

property freq¶: freq has been deprecated. See frequency for documentation

class SimPEG.electromagnetics.frequency_domain.sources.RawVec_e(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.sources.BaseFDEMSrc

RawVec electric source. It is defined by the user provided vector s_e

param list receiver_list

receiver list

param float freq

frequency

param numpy.ndarray s_e

electric source term

param bool integrate

Integrate the source term (multiply by Me) [False]

Required Properties:

frequency (Float): frequency of the source, a float in range [0, inf]
integrate (Boolean): integrate the source term?, a boolean, Default: False
receiver_list (a list of BaseRx): receiver list, a list (each item is an instance of BaseRx)

Optional Properties:

location (SourceLocationArray): Location of the source [x, y, z] in 3D, a 1D array denoting the source location of <class ‘float’>, <class ‘int’> with shape (*)

s_e(simulation)[source]¶

Electric source term

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: electric source term on mesh

class SimPEG.electromagnetics.frequency_domain.sources.RawVec_m(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.sources.BaseFDEMSrc

RawVec magnetic source. It is defined by the user provided vector s_m

param float freq

frequency

param receiver_list

receiver list

param numpy.ndarray s_m

magnetic source term

param bool integrate

Integrate the source term (multiply by Me) [False]

Required Properties:

frequency (Float): frequency of the source, a float in range [0, inf]
integrate (Boolean): integrate the source term?, a boolean, Default: False
receiver_list (a list of BaseRx): receiver list, a list (each item is an instance of BaseRx)

Optional Properties:

location (SourceLocationArray): Location of the source [x, y, z] in 3D, a 1D array denoting the source location of <class ‘float’>, <class ‘int’> with shape (*)

s_m(simulation)[source]¶

Magnetic source term

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: magnetic source term on mesh

class SimPEG.electromagnetics.frequency_domain.sources.RawVec(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.sources.BaseFDEMSrc

RawVec source. It is defined by the user provided vectors s_m, s_e

param receiver_list

receiver list

param float freq

frequency

param numpy.ndarray s_m

magnetic source term

param numpy.ndarray s_e

electric source term

param bool integrate

Integrate the source term (multiply by Me) [False]

Required Properties:

frequency (Float): frequency of the source, a float in range [0, inf]
integrate (Boolean): integrate the source term?, a boolean, Default: False
receiver_list (a list of BaseRx): receiver list, a list (each item is an instance of BaseRx)

Optional Properties:

location (SourceLocationArray): Location of the source [x, y, z] in 3D, a 1D array denoting the source location of <class ‘float’>, <class ‘int’> with shape (*)

s_m(simulation)[source]¶

Magnetic source term

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: magnetic source term on mesh

s_e(simulation)[source]¶

Electric source term

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: electric source term on mesh

class SimPEG.electromagnetics.frequency_domain.sources.MagDipole(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.sources.BaseFDEMSrc

Point magnetic dipole source calculated by taking the curl of a magnetic vector potential. By taking the discrete curl, we ensure that the magnetic flux density is divergence free (no magnetic monopoles!).

This approach uses a primary-secondary in frequency. Here we show the derivation for E-B formulation noting that similar steps are followed for the H-J formulation.

\[\begin{split}\mathbf{C} \mathbf{e} + i \omega \mathbf{b} = \mathbf{s_m} \\ {\mathbf{C}^T \mathbf{M_{\mu^{-1}}^f} \mathbf{b} - \mathbf{M_{\sigma}^e} \mathbf{e} = \mathbf{s_e}}\end{split}\]

We split up the fields and \(\mu^{-1}\) into primary (\(\mathbf{P}\)) and secondary (\(\mathbf{S}\)) components

\(\mathbf{e} = \mathbf{e^P} + \mathbf{e^S}\)

\(\mathbf{b} = \mathbf{b^P} + \mathbf{b^S}\)

\(\boldsymbol{\mu}^{\mathbf{-1}} = \boldsymbol{\mu}^{\mathbf{-1}^\mathbf{P}} + \boldsymbol{\mu}^{\mathbf{-1}^\mathbf{S}}\)

and define a zero-frequency primary simulation, noting that the source is generated by a divergence free electric current

\[\begin{split}\mathbf{C} \mathbf{e^P} = \mathbf{s_m^P} = 0 \\ {\mathbf{C}^T \mathbf{{M_{\mu^{-1}}^f}^P} \mathbf{b^P} - \mathbf{M_{\sigma}^e} \mathbf{e^P} = \mathbf{M^e} \mathbf{s_e^P}}\end{split}\]

Since \(\mathbf{e^P}\) is curl-free, divergence-free, we assume that there is no constant field background, the \(\mathbf{e^P} = 0\), so our primary problem is

\[\begin{split}\mathbf{e^P} = 0 \\ {\mathbf{C}^T \mathbf{{M_{\mu^{-1}}^f}^P} \mathbf{b^P} = \mathbf{s_e^P}}\end{split}\]

Our secondary problem is then

\[\begin{split}\mathbf{C} \mathbf{e^S} + i \omega \mathbf{b^S} = - i \omega \mathbf{b^P} \\ {\mathbf{C}^T \mathbf{M_{\mu^{-1}}^f} \mathbf{b^S} - \mathbf{M_{\sigma}^e} \mathbf{e^S} = -\mathbf{C}^T \mathbf{{M_{\mu^{-1}}^f}^S} \mathbf{b^P}}\end{split}\]

param list receiver_list

receiver list

param float freq

frequency

param numpy.ndarray location

source location (ie: np.r_[xloc,yloc,zloc])

param string orientation

‘X’, ‘Y’, ‘Z’

param float moment

magnetic dipole moment

param float mu

background magnetic permeability

Required Properties:

frequency (Float): frequency of the source, a float in range [0, inf]
integrate (Boolean): integrate the source term?, a boolean, Default: False
location (LocationVector): location of the source, A location array (1-dimensional numpy array) of <class ‘float’>, <class ‘int’> with shape (3), Default: [0. 0. 0.]
moment (Float): dipole moment of the transmitter, a float in range [0.0, inf], Default: 1.0
mu (Float): permeability of the background, a float in range [0.0, inf], Default: 1.25663706212e-06
orientation (Vector3): orientation of the source, a 3D Vector of <class ‘float’> with shape (3), Default: Z
receiver_list (a list of BaseRx): receiver list, a list (each item is an instance of BaseRx)

property moment¶: moment (Float): dipole moment of the transmitter, a float in range [0.0, inf], Default: 1.0

property mu¶: mu (Float): permeability of the background, a float in range [0.0, inf], Default: 1.25663706212e-06

property orientation¶: orientation (Vector3): orientation of the source, a 3D Vector of <class ‘float’> with shape (3), Default: Z

property loc¶: loc has been deprecated. See location for documentation

property location¶: location (LocationVector): location of the source, A location array (1-dimensional numpy array) of <class ‘float’>, <class ‘int’> with shape (3), Default: [0. 0. 0.]

bPrimary(simulation)[source]¶

The primary magnetic flux density from a magnetic vector potential

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary magnetic field

hPrimary(simulation)[source]¶

The primary magnetic field from a magnetic vector potential

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary magnetic field

s_m(simulation)[source]¶

The magnetic source term

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary magnetic field

s_e(simulation)[source]¶

The electric source term

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary magnetic field

s_eDeriv(simulation, v, adjoint=False)[source]¶

Derivative of electric source term with respect to the inversion model

Parameters

simulation (BaseFDEMSimulation) – FDEM Simulation
v (numpy.ndarray) – vector to take product with
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

product of electric source term derivative with a vector

class SimPEG.electromagnetics.frequency_domain.sources.MagDipole_Bfield(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.sources.MagDipole

Point magnetic dipole source calculated with the analytic solution for the fields from a magnetic dipole. No discrete curl is taken, so the magnetic flux density may not be strictly divergence free.

This approach uses a primary-secondary in frequency in the same fashion as the MagDipole.

param list receiver_list

receiver list

param float freq

frequency

param numpy.ndarray loc

source location (ie: np.r_[xloc,yloc,zloc])

param string orientation

‘X’, ‘Y’, ‘Z’

param float moment

magnetic dipole moment

param float mu

background magnetic permeability

Required Properties:

frequency (Float): frequency of the source, a float in range [0, inf]
integrate (Boolean): integrate the source term?, a boolean, Default: False
location (LocationVector): location of the source, A location array (1-dimensional numpy array) of <class ‘float’>, <class ‘int’> with shape (3), Default: [0. 0. 0.]
moment (Float): dipole moment of the transmitter, a float in range [0.0, inf], Default: 1.0
mu (Float): permeability of the background, a float in range [0.0, inf], Default: 1.25663706212e-06
orientation (Vector3): orientation of the source, a 3D Vector of <class ‘float’> with shape (3), Default: Z
receiver_list (a list of BaseRx): receiver list, a list (each item is an instance of BaseRx)

bPrimary(simulation)[source]¶

The primary magnetic flux density from the analytic solution for magnetic fields from a dipole

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary magnetic field

class SimPEG.electromagnetics.frequency_domain.sources.CircularLoop(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.sources.MagDipole

Circular loop magnetic source calculated by taking the curl of a magnetic vector potential. By taking the discrete curl, we ensure that the magnetic flux density is divergence free (no magnetic monopoles!).

This approach uses a primary-secondary in frequency in the same fashion as the MagDipole.

param list receiver_list

receiver list

param float freq

frequency

param numpy.ndarray loc

source location (ie: np.r_[xloc,yloc,zloc])

param string orientation

‘X’, ‘Y’, ‘Z’

param float moment

magnetic dipole moment

param float mu

background magnetic permeability

Required Properties:

current (Float): current in the loop, a float, Default: 1.0
frequency (Float): frequency of the source, a float in range [0, inf]
integrate (Boolean): integrate the source term?, a boolean, Default: False
location (LocationVector): location of the source, A location array (1-dimensional numpy array) of <class ‘float’>, <class ‘int’> with shape (3), Default: [0. 0. 0.]
mu (Float): permeability of the background, a float in range [0.0, inf], Default: 1.25663706212e-06
orientation (Vector3): orientation of the source, a 3D Vector of <class ‘float’> with shape (3), Default: Z
radius (Float): radius of the loop, a float in range [0.0, inf], Default: 1.0
receiver_list (a list of BaseRx): receiver list, a list (each item is an instance of BaseRx)

property radius¶: radius (Float): radius of the loop, a float in range [0.0, inf], Default: 1.0

property current¶: current (Float): current in the loop, a float, Default: 1.0

property moment¶: moment (Float): dipole moment of the transmitter, a float in range [0.0, inf], Default: 1.0

class SimPEG.electromagnetics.frequency_domain.sources.PrimSecSigma(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.sources.BaseFDEMSrc

Required Properties:

frequency (Float): frequency of the source, a float in range [0, inf]
integrate (Boolean): integrate the source term?, a boolean, Default: False
receiver_list (a list of BaseRx): receiver list, a list (each item is an instance of BaseRx)

Optional Properties:

location (SourceLocationArray): Location of the source [x, y, z] in 3D, a 1D array denoting the source location of <class ‘float’>, <class ‘int’> with shape (*)

s_e(simulation)[source]¶

Electric source term

Parameters: simulation (BaseFDEMSimulation) – FDEM Simulation
Return type: numpy.ndarray
Returns: electric source term on mesh

s_eDeriv(simulation, v, adjoint=False)[source]¶

Derivative of electric source term with respect to the inversion model

Parameters

simulation (BaseFDEMSimulation) – FDEM Simulation
v (numpy.ndarray) – vector to take product with
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

product of electric source term derivative with a vector

class SimPEG.electromagnetics.frequency_domain.sources.PrimSecMappedSigma(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.sources.BaseFDEMSrc

Primary-Secondary Source in which a mapping is provided to put the current model onto the primary mesh. This is solved on every model update. There are a lot of layers to the derivatives here!

Required :param list receiver_list: Receiver List :param float freq: frequency :param BaseFDEMSimulation primarySimulation: FDEM psimulation :param SurveyFDEM primarySurvey: FDEM primary survey

Optional :param Mapping map2meshSecondary: mapping current model to act as primary model on the secondary mesh

Required Properties:

frequency (Float): frequency of the source, a float in range [0, inf]
integrate (Boolean): integrate the source term?, a boolean, Default: False
receiver_list (a list of BaseRx): receiver list, a list (each item is an instance of BaseRx)

Optional Properties:

location (SourceLocationArray): Location of the source [x, y, z] in 3D, a 1D array denoting the source location of <class ‘float’>, <class ‘int’> with shape (*)

ePrimary(simulation, f=None)[source]¶

Primary electric field

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary electric field

ePrimaryDeriv(simulation, v, adjoint=False, f=None)[source]¶

Derivative of the primary electric field

Parameters

simulation (BaseFDEMSimulation) – FDEM simulation
v (numpy.ndarray) – vector
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

primary magnetic flux density

bPrimary(simulation, f=None)[source]¶

Primary magnetic flux density

Parameters: simulation (BaseFDEMSimulation) – FDEM simulation
Return type: numpy.ndarray
Returns: primary magnetic flux density

s_e(simulation, f=None)[source]¶

Electric source term

Parameters: simulation (BaseFDEMSimulation) – FDEM Simulation
Return type: numpy.ndarray
Returns: electric source term on mesh

s_eDeriv(simulation, v, adjoint=False)[source]¶

Derivative of electric source term with respect to the inversion model

Parameters

simulation (BaseFDEMSimulation) – FDEM Simulation
v (numpy.ndarray) – vector to take product with
adjoint (bool) – adjoint?

Return type

numpy.ndarray

Returns

product of electric source term derivative with a vector

class SimPEG.electromagnetics.frequency_domain.receivers.BaseRx(*args, **kwargs)[source]¶

Bases: SimPEG.survey.BaseRx

Frequency domain receiver base class

param numpy.ndarray locations

receiver locations (ie. np.r_[x,y,z])

param string orientation

receiver orientation ‘x’, ‘y’ or ‘z’

param string component

real or imaginary component ‘real’ or ‘imag’

Required Properties:

component (StringChoice): component of the field (real or imag), either “real” or “imag”
locations (RxLocationArray): Locations of the receivers (nRx x nDim), an array of receiver locations of <class ‘float’>, <class ‘int’> with shape (*, *)
orientation (StringChoice): orientation of the receiver. Must currently be ‘x’, ‘y’, ‘z’, any of “x”, “y”, “z”
storeProjections (Boolean): Store calls to getP (organized by mesh), a boolean, Default: True

property projComp¶: projComp has been deprecated. See orientation for documentation

property orientation¶: orientation (StringChoice): orientation of the receiver. Must currently be ‘x’, ‘y’, ‘z’, any of “x”, “y”, “z”

property component¶: component (StringChoice): component of the field (real or imag), either “real” or “imag”

projGLoc(f)[source]¶: Grid Location projection (e.g. Ex Fy …)

eval(src, mesh, f)[source]¶

Project fields to receivers to get data.

Parameters

src (SimPEG.electromagnetics.frequency_domain.sources.BaseFDEMSrc) – FDEM source
mesh (discretize.base.BaseMesh) – mesh used
f (Fields) – fields object

Return type

numpy.ndarray

Returns

fields projected to recievers

evalDeriv(src, mesh, f, du_dm_v=None, v=None, adjoint=False)[source]¶

Derivative of projected fields with respect to the inversion model times a vector.

Parameters

src (SimPEG.electromagnetics.frequency_domain.sources.BaseFDEMSrc) – FDEM source
mesh (discretize.base.BaseMesh) – mesh used
f (Fields) – fields object
v (numpy.ndarray) – vector to multiply

Return type

numpy.ndarray

Returns

fields projected to recievers

class SimPEG.electromagnetics.frequency_domain.receivers.PointElectricField(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.receivers.BaseRx

Electric field FDEM receiver

param numpy.ndarray locations

receiver locations (ie. np.r_[x,y,z])

param string orientation

receiver orientation ‘x’, ‘y’ or ‘z’

param string component

real or imaginary component ‘real’ or ‘imag’

Required Properties:

component (StringChoice): component of the field (real or imag), either “real” or “imag”
locations (RxLocationArray): Locations of the receivers (nRx x nDim), an array of receiver locations of <class ‘float’>, <class ‘int’> with shape (*, *)
orientation (StringChoice): orientation of the receiver. Must currently be ‘x’, ‘y’, ‘z’, any of “x”, “y”, “z”
storeProjections (Boolean): Store calls to getP (organized by mesh), a boolean, Default: True

class SimPEG.electromagnetics.frequency_domain.receivers.PointMagneticFluxDensity(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.receivers.BaseRx

Magnetic flux FDEM receiver

param numpy.ndarray locations

receiver locations (ie. np.r_[x,y,z])

param string orientation

receiver orientation ‘x’, ‘y’ or ‘z’

param string component

real or imaginary component ‘real’ or ‘imag’

Required Properties:

component (StringChoice): component of the field (real or imag), either “real” or “imag”
locations (RxLocationArray): Locations of the receivers (nRx x nDim), an array of receiver locations of <class ‘float’>, <class ‘int’> with shape (*, *)
orientation (StringChoice): orientation of the receiver. Must currently be ‘x’, ‘y’, ‘z’, any of “x”, “y”, “z”
storeProjections (Boolean): Store calls to getP (organized by mesh), a boolean, Default: True

class SimPEG.electromagnetics.frequency_domain.receivers.PointMagneticFluxDensitySecondary(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.receivers.BaseRx

Magnetic flux FDEM receiver

param numpy.ndarray locations

receiver locations (ie. np.r_[x,y,z])

param string orientation

receiver orientation ‘x’, ‘y’ or ‘z’

param string component

real or imaginary component ‘real’ or ‘imag’

Required Properties:

component (StringChoice): component of the field (real or imag), either “real” or “imag”
locations (RxLocationArray): Locations of the receivers (nRx x nDim), an array of receiver locations of <class ‘float’>, <class ‘int’> with shape (*, *)
orientation (StringChoice): orientation of the receiver. Must currently be ‘x’, ‘y’, ‘z’, any of “x”, “y”, “z”
storeProjections (Boolean): Store calls to getP (organized by mesh), a boolean, Default: True

class SimPEG.electromagnetics.frequency_domain.receivers.PointMagneticField(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.receivers.BaseRx

Magnetic field FDEM receiver

param numpy.ndarray locations

receiver locations (ie. np.r_[x,y,z])

param string orientation

receiver orientation ‘x’, ‘y’ or ‘z’

param string component

real or imaginary component ‘real’ or ‘imag’

Required Properties:

component (StringChoice): component of the field (real or imag), either “real” or “imag”
locations (RxLocationArray): Locations of the receivers (nRx x nDim), an array of receiver locations of <class ‘float’>, <class ‘int’> with shape (*, *)
orientation (StringChoice): orientation of the receiver. Must currently be ‘x’, ‘y’, ‘z’, any of “x”, “y”, “z”
storeProjections (Boolean): Store calls to getP (organized by mesh), a boolean, Default: True

class SimPEG.electromagnetics.frequency_domain.receivers.PointCurrentDensity(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.receivers.BaseRx

Current density FDEM receiver

param numpy.ndarray locations

receiver locations (ie. np.r_[x,y,z])

param string orientation

receiver orientation ‘x’, ‘y’ or ‘z’

param string component

real or imaginary component ‘real’ or ‘imag’

Required Properties:

component (StringChoice): component of the field (real or imag), either “real” or “imag”
locations (RxLocationArray): Locations of the receivers (nRx x nDim), an array of receiver locations of <class ‘float’>, <class ‘int’> with shape (*, *)
orientation (StringChoice): orientation of the receiver. Must currently be ‘x’, ‘y’, ‘z’, any of “x”, “y”, “z”
storeProjections (Boolean): Store calls to getP (organized by mesh), a boolean, Default: True

class SimPEG.electromagnetics.frequency_domain.receivers.Point_e(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.receivers.PointElectricField

This class has been deprecated, see PointElectricField for documentation

class SimPEG.electromagnetics.frequency_domain.receivers.Point_b(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.receivers.PointMagneticFluxDensity

This class has been deprecated, see PointMagneticFluxDensity for documentation

class SimPEG.electromagnetics.frequency_domain.receivers.Point_bSecondary(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.receivers.PointMagneticFluxDensitySecondary

This class has been deprecated, see PointMagneticFluxDensitySecondary for documentation

class SimPEG.electromagnetics.frequency_domain.receivers.Point_h(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.receivers.PointMagneticField

This class has been deprecated, see PointMagneticField for documentation

class SimPEG.electromagnetics.frequency_domain.receivers.Point_j(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.receivers.PointCurrentDensity

This class has been deprecated, see PointCurrentDensity for documentation

FDEM Fields¶

class SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM(*args, **kwargs)[source]¶

Bases: SimPEG.fields.Fields

Fancy Field Storage for a FDEM survey. Only one field type is stored for each problem, the rest are computed. The fields object acts like an array and is indexed by
f = problem.fields(m)
e = f[source_list,'e']
b = f[source_list,'b']
If accessing all sources for a given field, use the :
f = problem.fields(m)
e = f[:,'e']
b = f[:,'b']
The array returned will be size (nE or nF, nSrcs \(\times\) nFrequencies)

Required Properties:

aliasFields (Dictionary):
a dictionary of the aliased fields with [alias, location, function], e.g. {“b”:[“e”,”F”,lambda(F,e,ind)]} , a dictionary
simulation (BaseSimulation): a SimPEG simulation, an instance of BaseSimulation

knownFields = {}¶

dtype¶: alias of builtins.complex

class SimPEG.electromagnetics.frequency_domain.fields.Fields3DElectricField(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM

Fields object for Simulation3DElectricField.

param discretize.base.BaseMesh mesh

mesh

param SimPEG.electromagnetics.frequency_domain.SurveyFDEM.Survey survey

survey

Required Properties:

simulation (BaseSimulation): a SimPEG simulation, an instance of BaseSimulation

knownFields = {'eSolution': 'E'}¶

aliasFields = {'b': ['eSolution', 'F', '_b'], 'bPrimary': ['eSolution', 'F', '_bPrimary'], 'bSecondary': ['eSolution', 'F', '_bSecondary'], 'e': ['eSolution', 'E', '_e'], 'ePrimary': ['eSolution', 'E', '_ePrimary'], 'eSecondary': ['eSolution', 'E', '_eSecondary'], 'h': ['eSolution', 'F', '_h'], 'j': ['eSolution', 'E', '_j']}¶

startup()[source]¶

class SimPEG.electromagnetics.frequency_domain.fields.Fields3DMagneticFluxDensity(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM

Fields object for Simulation3DMagneticFluxDensity.

param discretize.base.BaseMesh mesh

mesh

param SimPEG.electromagnetics.frequency_domain.SurveyFDEM.Survey survey

survey

Required Properties:

simulation (BaseSimulation): a SimPEG simulation, an instance of BaseSimulation

knownFields = {'bSolution': 'F'}¶

aliasFields = {'b': ['bSolution', 'F', '_b'], 'bPrimary': ['bSolution', 'F', '_bPrimary'], 'bSecondary': ['bSolution', 'F', '_bSecondary'], 'e': ['bSolution', 'E', '_e'], 'ePrimary': ['bSolution', 'E', '_ePrimary'], 'eSecondary': ['bSolution', 'E', '_eSecondary'], 'h': ['bSolution', 'F', '_h'], 'j': ['bSolution', 'E', '_j']}¶

startup()[source]¶

class SimPEG.electromagnetics.frequency_domain.fields.Fields3DCurrentDensity(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM

Fields object for Simulation3DCurrentDensity.

param discretize.base.BaseMesh mesh

mesh

param SimPEG.electromagnetics.frequency_domain.SurveyFDEM.Survey survey

survey

Required Properties:

simulation (BaseSimulation): a SimPEG simulation, an instance of BaseSimulation

knownFields = {'jSolution': 'F'}¶

aliasFields = {'b': ['jSolution', 'E', '_b'], 'e': ['jSolution', 'F', '_e'], 'h': ['jSolution', 'E', '_h'], 'hPrimary': ['jSolution', 'E', '_hPrimary'], 'hSecondary': ['jSolution', 'E', '_hSecondary'], 'j': ['jSolution', 'F', '_j'], 'jPrimary': ['jSolution', 'F', '_jPrimary'], 'jSecondary': ['jSolution', 'F', '_jSecondary']}¶

startup()[source]¶

class SimPEG.electromagnetics.frequency_domain.fields.Fields3DMagneticField(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEM

Fields object for Simulation3DMagneticField.

param discretize.base.BaseMesh mesh

mesh

param SimPEG.electromagnetics.frequency_domain.SurveyFDEM.Survey survey

survey

Required Properties:

simulation (BaseSimulation): a SimPEG simulation, an instance of BaseSimulation

knownFields = {'hSolution': 'E'}¶

aliasFields = {'b': ['hSolution', 'CCV', '_b'], 'e': ['hSolution', 'CCV', '_e'], 'h': ['hSolution', 'E', '_h'], 'hPrimary': ['hSolution', 'E', '_hPrimary'], 'hSecondary': ['hSolution', 'E', '_hSecondary'], 'j': ['hSolution', 'F', '_j'], 'jPrimary': ['hSolution', 'F', '_jPrimary'], 'jSecondary': ['hSolution', 'F', '_jSecondary']}¶

startup()[source]¶

class SimPEG.electromagnetics.frequency_domain.fields.Fields3D_e(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.fields.Fields3DElectricField

This class has been deprecated, see Fields3DElectricField for documentation

class SimPEG.electromagnetics.frequency_domain.fields.Fields3D_b(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.fields.Fields3DMagneticFluxDensity

This class has been deprecated, see Fields3DMagneticFluxDensity for documentation

class SimPEG.electromagnetics.frequency_domain.fields.Fields3D_j(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.fields.Fields3DCurrentDensity

This class has been deprecated, see Fields3DCurrentDensity for documentation

class SimPEG.electromagnetics.frequency_domain.fields.Fields3D_h(*args, **kwargs)[source]¶

Bases: SimPEG.electromagnetics.frequency_domain.fields.Fields3DMagneticField

This class has been deprecated, see Fields3DMagneticField for documentation